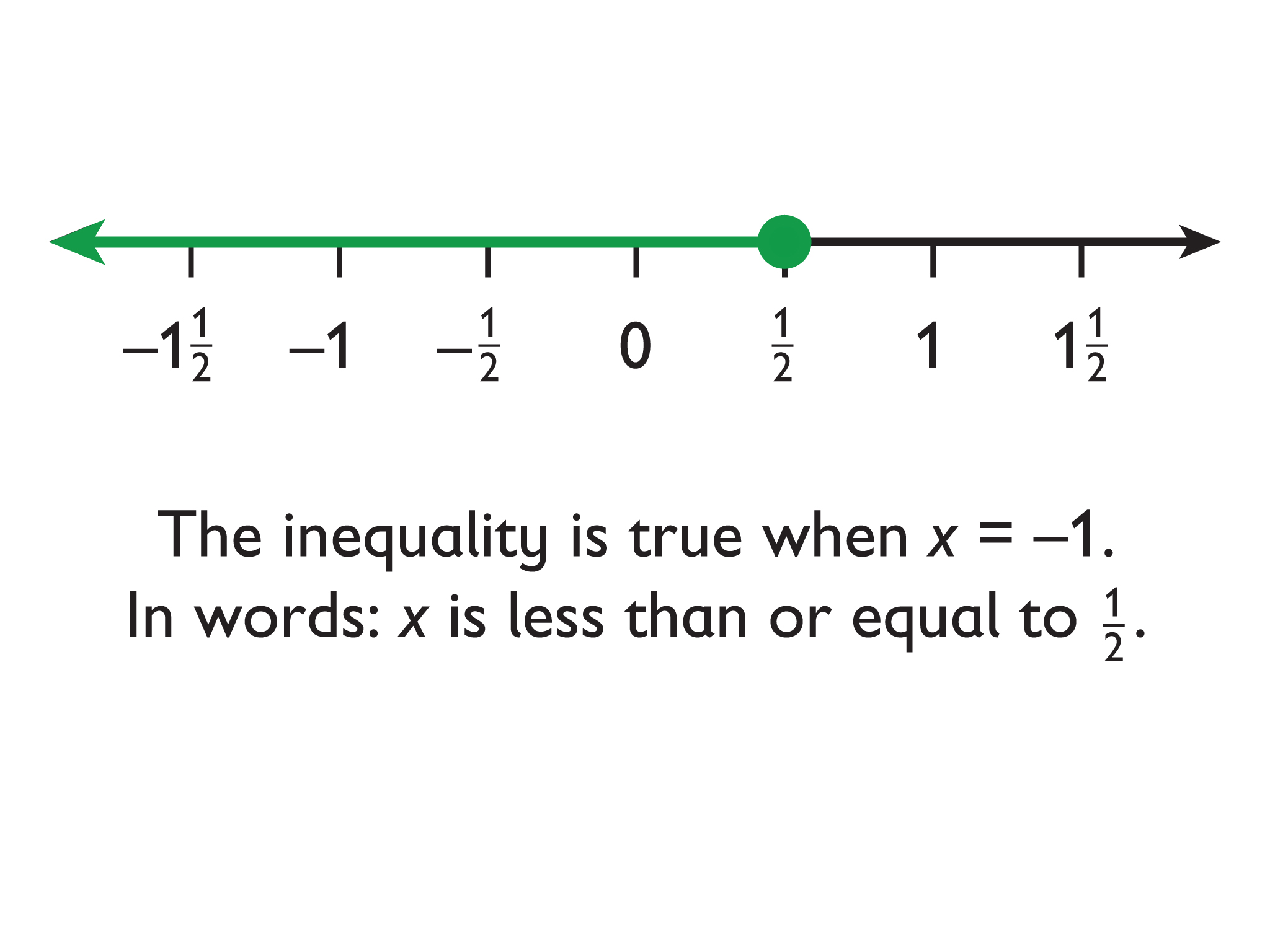- Subject:
- Numbers and Operations
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 6
- Provider:
- Pearson
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Text/HTML
Education Standards
Match Inequalities to Graphs
Representing An Inequality On A Number Line

Overview
Lesson Overview
Students represent inequalities on a number line, find at least one value that makes the inequality true, and write the inequality using words.
SWD:When calling on students, be sure to call on ELLs and to encourage them to actively participate. Understand that their pace might be slower or they might be shy or more reluctant to volunteer due to their weaker command of the language.
SWD:Thinking aloud is one strategy for making learning visible. When teachers think aloud, they are externalizing their internal thought processes. Doing so may provide students with insights into mathematical thinking and ways of tackling problems. It also helps to model accurate mathematical language.
Key Concepts
Inequalities, like equations, have solutions. An arrow on the number line—pointing to the right for greater values and to the left for lesser values—can be used to show that there are infinitely many solutions to an inequality.
The solutions to x < a are represented on the number line by an arrow pointing to the left from an open circle at a.
Example: x < 2
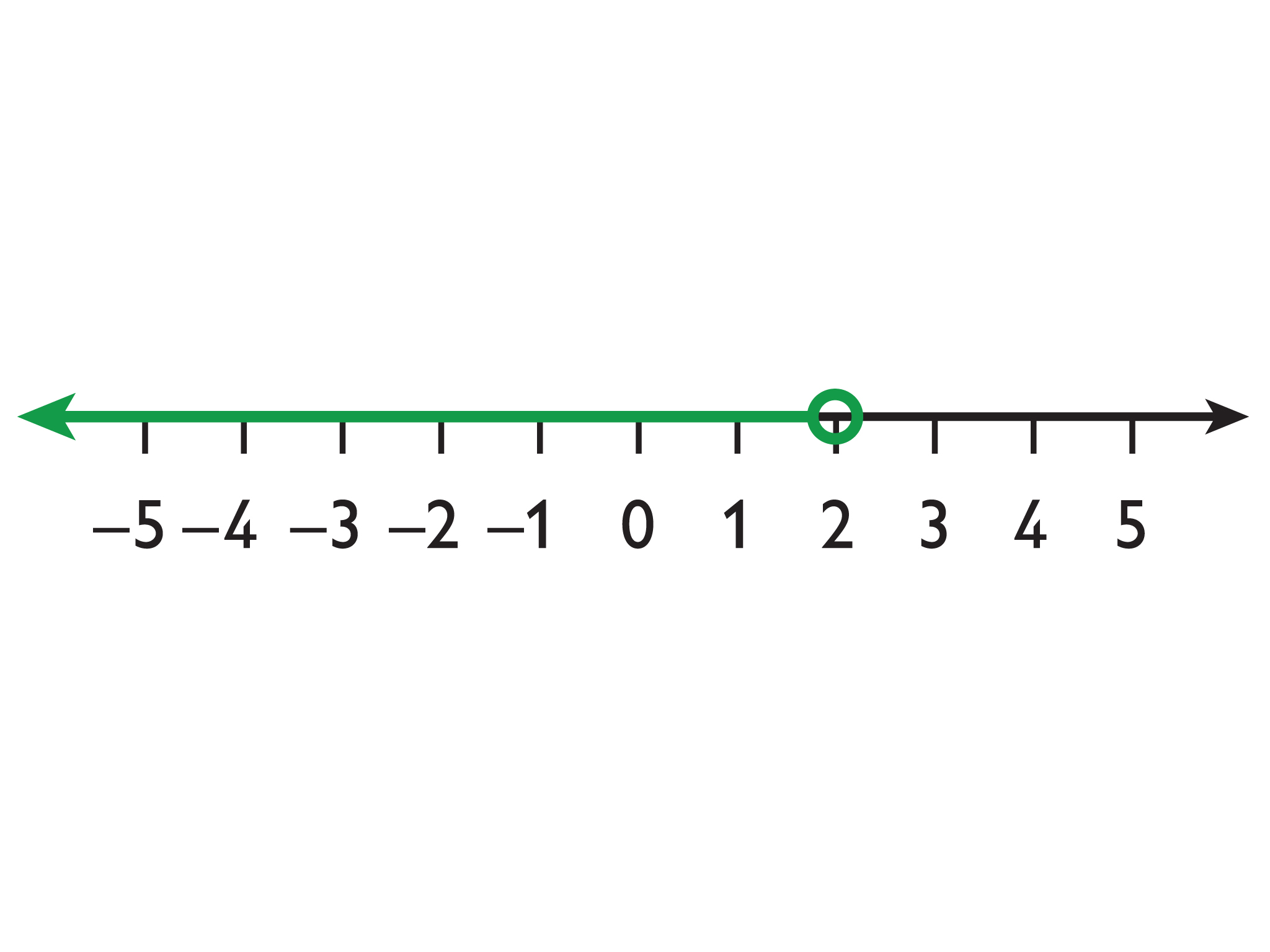
The solutions to x > a are represented on the number line with an arrow pointing to the right from an open circle at a.
Example: x > 2

The solutions to x ≤ a are represented on the number line with an arrow pointing to the left from a closed circle at a.
Example: x ≤ 2

The solutions to x ≥ a are represented on the number line with an arrow pointing to the right from a closed circle at a.
Example: x ≥ 2

Goals and Learning Objectives
- Represent an inequality on a number line and using words.
- Understand that inequalities have infinitely many solutions.
Match Inequalities to Graphs
Lesson Guide
Have students work in pairs to match the inequalities with their representations on the number line and to write the inequality in words.
Share the inequalities from the Opening and the correct corresponding number line graphs with the students so they can easily reference them in the future.
ELL: Learning new ways of graphing inequalities can be a challenge for ELLs. Preview and/or pre-teach the new concepts in this lesson. Promote connections to students' background knowledge and to previous lessons in this unit.
Mathematics
Students will use reasoning to match the number lines with the correct inequalities. They will need to reason that the open circle means that the number is not included in the inequality and the closed circle indicates that it is included. Do not provide this information for the students. If the class does not all agree on this convention initially, allow students to defend their positions until all see why this convention makes sense.
- x < 2: B. "x is less than 2."
- x > 2: C. "x is greater than 2."
- x ≥ 2: D. "x is greater than or equal to 2."
- x ≤ : A. "x is less than or equal to 2."
Opening
Match Inequalities to Graphs
- Match each inequality to a number line.
- Write the inequality in words in the space provided; for example, "x is less than 5."
INTERACTIVE: Match Inequalities to Graphs
Math Mission
Lesson Guide
Discuss the Math Mission. Students will represent inequalities on a number line and find at least one value that makes the inequality true.
Opening
Represent inequalities on a number line and find at least one value that makes the inequality true.
Inequalities and Number Lines
Lesson Guide
Have students work in pairs on the problems in Tasks 3 and 4. Identify any student misconceptions to address in Ways of Thinking.
SWD: Circulate through your classroom before your students share. Help students to identify ideas from their notes and thoughts that are appropriate to contribute during this portion of the Ways of Thinking discussion.
Mathematical Practices
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Listen for student conversations about whether rules or conventions apply the same way to negative values as they do to positive values.
Mathematical Practice 6: Attend to precision.
Listen for student conversations about whether the circles should be open or closed.
Listen for student conversations about which direction the arrows should face.
Interventions
Student does not understand how to use the interactive.
- Ask your partner to demonstrate how to use the interactive.
Student struggles with negative values and the direction of arrows.
- Is the number to the left greater than or less than the number to its right?
Student is confused about the conventions for using open and closed circles on the number line.
- Look back at the answers to the Opening.
- How are the math conventions connected to language: greater than or less than, and greater than or equal to or less than or equal to?
Student does not know how to find one value that makes the inequality true.
- Look at the open (or closed) circle. Does that number make the inequality true?
- Will the numbers that make the inequality true be to the left or right of the open (or closed) circle?
Answers
Work Time
Inequalities and Number Lines
For each inequality do the following.
- Represent the inequality on a number line using the number line interactive.
- Write one value that makes the inequality true.
- Write the inequality using words.
- x ≥ –2
- x < 4
- 12 ≥ x
- x ≤ −3.5
- x < 1.5
INTERACTIVE: Inequalities and Number Lines
Hint:
- Where is the number located on the number line?
- Should the starting point be a closed circle or an open circle?
- What is one value that makes the inequality true? Is that value shaded on the number line?
Write About the Number Line
Lesson Guide
Watch for students who:
- Cannot write a real-world situation to represent the number line.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Look for a variety of real-world scenarios.
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
Listen for student conversations about whether rules or conventions apply the same way to negative values as they do to positive values.
Possible Answers:
- Children must be at least 5 years old to attend the story hour.
- The minimum price of a T-shirt in that store is $5.
- That box of books weighs 5 lb or more.
Work Time
Write About the Number Line
- Write about a real-world situation that could be represented by this number line.

Hint:
Think about situations involving age, money, or weight.
Prepare a Presentation
Preparing for Ways of Thinking
Watch for students who:
- Incorrectly use the open and closed circles on the number line diagram to represent the inequality statements.
- Show the arrow in the wrong direction on their number line diagrams.
- Have trouble working with negative values.
- Have trouble when the variable is on the right side of the inequality symbol.
- Cannot identify a value that makes the inequality true.
- Cannot accurately write the inequality using words.
- Cannot write a real-world situation to represent the number line diagram.
Step 1: Work Time
Prepare a Presentation
- Explain how you represented an inequality on a number line.
- Support your explanation with your work.
Challenge Problem
Possible Answers:
- I do not agree; -2 is not less than -5. I know that -2 is greater than -5 because -2 is to the right of -5 on the number line.

Step 2: Work Time
Challenge Problem
Denzel says that because 2<5, that means −2<−5.
- Do you agree? Explain why or why not.
Make Connections
Lesson Guide
Highlight the fact that the arrows on the number lines in the first problem represent solutions to the inequality statements, and facilitate recognition that there are infinitely many solutions to each inequality.
Ask students:
- How many solutions do these statements have?
- Why do you use a line with an arrow to represent these solutions?
Draw on ideas and diagrams from one or two students who worked on the Challenge Problem. Focus on 2 < 5 and −2 > −5 to frame the first part of the Ways of Thinking discussion.
Ask students:
- How does the number line help you understand what is going on?
- Which is greater, –10 or –10.5? Represent these numbers on the number line. Then compare your results with the inequality statement 10 < 10.5.
For the rest of the discussion, focus on situations to match the number line, allowing as many students as possible to share their real-world situations.
ELL: As with other oral instructions, ensure that the pace of your speech is appropriate for ELLs. Pause frequently to allow students to pose questions. Alternatively, monitor students' understanding by asking questions as your explanation unfolds.
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates’ representations of inequalities on a number line.
Hint:
As your classmates present, ask questions such as:
- Why is the circle filled in?
- Why is the circle open?
- Why does the line go in that direction?
- Explain why –4 is less than –3.5.
- What is the greatest number that x could be?
Inequalities
Lesson Guide
Have pairs quietly discuss the information about inequalities. Have them give additional examples of real-world situations for each type of inequality.
As student pairs work together, listen for students who may still have misconceptions so you can address them in the class discussion.
After a few minutes, discuss the Summary as a class. Review the following points.
Mathematics
Inequalities, like equations, have solutions.
An arrow on the number line—pointing to the right for greater values and to the left for lesser values—can be used to show that there are infinitely many solutions to an inequality.
The solutions to x < ax < a (xx is less than aa) are represented on the number line by an arrow pointing to the left from an open circle at aa.
The solutions to x > ax > a (xx is greater than aa) are represented on the number line with an arrow pointing to the right from an open circle at aa.
The solutions to x ≤ ax ≤ a (xx is less than or equal to aa) are represented on the number line with an arrow pointing to the left from a closed circle at aa.
The solutions to x ≥ ax ≥ a (xx is greater than or equal to aa) are represented on the number line with an arrow pointing to the right from a closed circle at aa.
Formative Assessment
Summary of the Math: Inequalities
Read and Discuss
An inequality is a relationship that holds between two values that are different.
a < b means that a is less than b (or, equivalently, that b is greater than a).
a > b means that a is greater than b (or, equivalently, that b is less than a).
a ≤ b means that a is less than or equal to b (or, equivalently, that b is greater than or equal to a).
a ≥ b means that a is greater than or equal to b (or, equivalently, that b is less than or equal to a).

Hint:
Can you:
- Explain the meaning of each inequality symbol?
- Show how each type of inequality is represented on a number line?
Solve and Use Equations
Lesson Guide
This task allows you to assess students’ work and determine what difficulties they are having. The results of the Self Check will help you determine which students should work on the Gallery and which students would benefit from review before the assessment. Have students work on the Self Check individually.
Assessment
Have students submit their work to you. Make notes on what their work reveals about their current levels of understanding and their different problem-solving approaches.
Do not score students’ work. Share with each student the most appropriate Interventions to guide their thought process. Also note students with a particular issue so that you can work with them in the Putting It Together lesson that follows.
SWD: Post the Interventions in the classroom for students to use as a resource as they work. Create and provide an enhanced version of the Interventions with embedded text structures (labels, highlights, words in bold) to cue students to pay closer attention to particular terms.
Interventions
Student uses the wrong property or identifies the property incorrectly.
- Use the addition property of equality for equations like x + 4 = 10.
- Use the multiplication property of equality for equations like 2x = 10 or 12x = 9 or for solving proportions.
Student solves the equation incorrectly.
- Did you use the correct operation to isolate x?
- Did you substitute the solution into the equation to check it?
Student does not include any word problems.
- Try these starters:
- A shirt costs $5 more than a …
- Four books cost $22 …
- A purple paint is mixed in the ratio of …
Student's word problem does not match the equation given.
- Work backwards. Read the word problem you wrote. Write an equation that represents it. Does it match the equation you were given?
Answers
Word problems will vary. Possible answer: A shirt costs $5 more than a pair of shorts. The shirt costs $17. How much does the pair of shorts cost? Answer: The pair of shorts costs $12.
Word problems will vary. Possible answer: Four books cost $22. Each costs the same amount. How much does one book cost? Answer: One book costs $5.50.
Word problems will vary. Possible answer: A purple paint is mixed in the ratio of 5 parts blue to 8 parts red. How much blue paint should be mixed with 6 cups of red paint to get the same shade of purple? Answer: You should mix 3 cups of blue paint.
Formative Assessment
Solve and Use Equations
Complete this Self Check by yourself.
For each equation do the following.
- Solve the equation. Name the property of equality you use and show each step.
- Write and solve a word problem that each equation could represent.
- x + 5 = 17
- 4x = 22
Reflect On Your Work
Lesson Guide
Have each student write a quick reflection before the end of the class. Review the reflections to learn where students see inequalities in real-world situations outside of the classroom.
Work Time
Reflect On Your Work
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
One place outside of the classroom where I have seen inequalities is …