Division

Overview
Students use models and the idea of dividing as making equal groups to divide a fraction by a whole number.
SWD: Some students with disabilities will benefit from a preview of the goals in each lesson. Students can highlight the critical features or concepts in order to help them pay close attention to salient information.
Key Concepts
When we divide a whole number by a whole number n, we can think of making n equal groups and finding the size of each group. We can think about dividing a fraction by a whole number in the same way.
8 ÷ 4 = 2
When we make 4 equal groups, there are 2 wholes in each group.
When we make 4 equal groups, there are 2 ninths in each group.
When the given fraction cannot be divided into equal groups of unit fractions, we can break each unit fraction part into smaller parts to form an equivalent fraction.
÷ 6 = ? ÷ 6 = ? ÷ 6 =
Students see that, in general, we can divide a fraction by a whole number by dividing the numerator by the whole number. Note that this is consistent with the “multiply by the reciprocal” method.
Goals and Learning Objectives
- Use models to divide a fraction by a whole number.
- Learn general methods for dividing a fraction by a whole number without using a model.
Divide Objects into Groups
Lesson Guide
Students should discuss the question with their partner. Remind the class that they do not have to solve the problem, just discuss possible strategies.
SWD: Point to or highlight the piece of the number line that you are referring to so that students can follow along as you represent on your number line.
Opening
Divide Objects into Groups
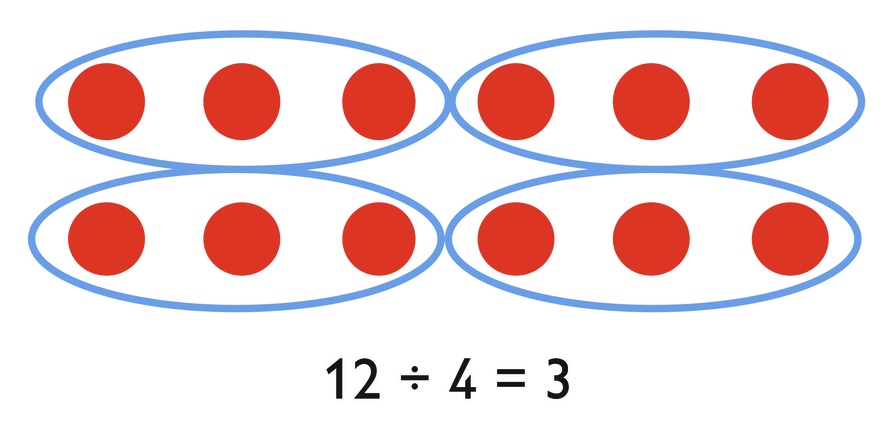
You can find 12 ÷ 4 by dividing 12 objects into 4 equal groups.
- How can you use a similar method to find ?
- Discuss this question with your partner.
Math Mission
Lesson Guide
Discuss the Math Mission. Students will devise strategies for dividing a fraction by a whole number.
ELL: Posters are a type of graphic organizer that help ELLs see mathematical connections, as well as illustrate and clarify new concepts, vocabulary, and background knowledge necessary for mathematical learning.
Opening
Devise strategies for dividing a fraction by a whole number.
Mia’s Models
Lesson Guide
Briefly discuss the two models for shown—a bar model and a number line model. Tell students they can use one of the given models or draw one of their own. Then ask students to work with their partners on the problems.
Mathematics
If students have trouble getting started, refer them to the whole-number division problem in the Opening in which 12 objects were divided into 4 equal groups. Tell students that they can think of each of the 8 ninths as an object. How can they divide these 8 ninths into 4 equal groups?
Interventions
Student has difficulty working with the models.
- Choose one of the models for , or create your own. Can you explain how it shows ?
- To find ÷ 4, you must divide into four equal groups or four equal parts. Can you see from the model how you can do this?
- Think of each ninth as one “object.” So, you have 8 objects, and you are dividing them into four groups. How many objects are in each group?
Student finds an incorrect quotient.
- How can you use multiplication to check your answer?
- is close to 1. If you divide it into 4 parts, about how big should each part be? Does your answer seem reasonable?
Answers
- (Models will vary.)
- ÷ 4 =
- Check: 4 × =
Work Time
Mia’s Models
Mia wants to divide by 4. She draws two different models to represent the fraction .
Use one of Mia’s models of , or make your own model of the fraction, to help you solve the problem.
- Divide by 4.
- Write a division equation to represent what you did.
- Use multiplication to check your answer.
Can you divide your model into 4 equal parts? What is the size of each part?
Juice
Mathematics
Students may struggle with the juice problem because it is not immediately obvious how to divide the quart into 6 equal groups. Remind them that there are lots of fractions that are equivalent to .
- How can we change the model to make an equivalent fraction?
- Is one of these equivalent fractions easier to divide by 6 than the original fraction?
- Is there a way other than a bar or number line model to represent this problem?
Some methods for solving ÷ 6:
- Model using a circular area, bar, or number line model. Then divide each fourth into 2 equal parts to get eighths. Divide the 6 eighths that are shaded into 6 groups. There is 1 eighth in each group.
So, ÷ 6 = ÷ 6 = .
Possible models:
Area Model
Bar Model
Number Line
- Write as . We know that = + + + + + . Because is the sum of six s, when we divide it by 6, we get one .
- Write the division as an inverse multiplication: × = = .
[common error] Students might think that the total number of parts (the denominator of the fraction) must be divisible by 6 and divide each fourth into 3 equal parts to get twelfths. This will give 9 shaded parts (the model will represent ), which cannot be divided into 6 equal groups. Remind these students that they are dividing only the shaded parts (represented by the numerator of the fraction) into 6 groups.
SWD: Students with disabilities may struggle to self-monitor whether strategies are effective or ineffective. If students are demonstrating difficulty shifting gears from an ineffective strategy, model think-aloud strategies to help students reflect.
Interventions
Student does not see how to divide 3/4 into 6 parts.
- Remember that there are lots of fractions that are equivalent to . Maybe one of them is easier to divide into 6 parts.
- What if you break each of the fourths in your model into 2 equal parts?
- What fraction would the shaded part represent?
- Is this fraction equivalent to ?
- Can you divide this new fraction into 6 parts?
Student finds an incorrect quotient.
- How can you use multiplication to check your answer?
- If you divide into 6 parts, will each part be bigger or smaller than ? Will it be much smaller or just a little smaller? Does your answer seem reasonable?
Answers
- ÷ 6 =
- Models will vary (see models above).
- Methods will vary.
- Check: 6 × = =
Work Time
Juice
There is quart of juice left in a carton. If the 6 members of the Nelson family share the juice equally, how much (in quarts) will each person get?
- Write the division expression that you need to solve this problem.
- Make a model.
- Use your model, or use a method that does not involve a model if you prefer, to solve the problem.
- Use multiplication to check your answer.
Can you find an equivalent fraction for 3 4 that is easy to divide into 6 equal parts?
Carlos’s Method
Mathematical Practices
Mathematical Practice 2: Reason abstractly and quantitatively.
Partners should discuss the concept of inverse operations, why it works for Carlos, and why it might work for their problem. It should also be discussed as a class during Ways of Thinking.
Interventions
If students are having difficulties:
- What was Carlos dividing by and what you are dividing by?
- What did Carlos do?
- What is the inverse of 3?
Answers
- Check: 3 × =
Work Time
Carlos’s Method
Carlos knows that division and multiplication are inverse operations. He knows, for example, that dividing by 4 is the same as multiplying by . He thinks that he can use this inverse relationship to help him divide a fraction by a whole number.
To solve ÷ 4, Carlos writes the expression × . He multiplies to get , and then simplifies to the equivalent fraction . Carlos writes this answer: ÷ 4 = .
- Use Carlos’s method to solve ÷ 3.
- Use multiplication to check your answer.
Prepare a Presentation
Preparing for Ways of Thinking
Choose solutions that use a variety of models and methods to be presented during Ways of Thinking. Also select some students who solved the Challenge Problem to present during Ways of Thinking.
Presentations will vary. They should include an explanation of each problem and a comparison of the three problems.
Challenge Problem
Answers
- (Problems will vary.)
Work Time
Prepare a Presentation
- Explain how you solved each problem.
- Provide a comparison of the three problems.
- What is similar about the problems?
- What is different about the problems?
Challenge Problem
- Create a real-world problem that can be solved by finding .
Make Connections
Lesson Guide
Have students who used different methods to solve the problems present their solutions. For the juice problem, be sure a variety of models are presented as well as solutions that do not use models.
Present students with the problem . Point out that in this problem, we are dividing a mixed number by a whole number. To use Carlos’s method, we have to rewrite the mixed number as a fraction:
Alternatively, we can rewrite the mixed number as a fraction where the numerator is divisible by 2:
Check:
This can also be represented with a bar model:
Draw a model. 1 is the same as .
5 thirds cannot be divided by 2, so break each third into 2 parts to get 10 sixths.
The 10 sixths can be divided into 2 groups of 5 sixths, so 1 ÷ 2 = .
You might also demonstrate that the modeling process for this problem is the same as when we divide a fraction by a whole number.
ELL: In facilitating the discussion, provide an appropriate pace and ample wait time to allow for thoughtful participation by ELLs. Present key words in writing, and allow students to use dictionaries before responding. Also allow students to use diagrams to aid in their explanation.
Additionally, if the language proficiency of some of the students is low, present sentence frames to help them with the structure of the sentences.
Mathematical Practices
Mathematical Practice 8: Look for and express regularity in repeated reasoning.
During the presentations, focus on the similarities between the problems. Ask if there is a method (or methods) that could have been used for all three problems.
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates’ methods for dividing a fraction by a whole number.
As your classmates present, ask questions such as:
- Where in your model do you see the total amount that you divided into equal groups?
- Where in your model do you see the number of equal groups?
- Where in your model do you see the size of each group?
- How can you use what you know about equivalent fractions to make the problem easier?
- What do you know about the relationship between multiplication and division? How can this relationship help you solve the problem?
Divide Fractions by Whole Numbers
Lesson Guide
Challenge students to use a method that they had not used in the Work Time problems. For students who are fluent in multiple methods, challenge them to create real-world problems. Have students work alone.
Answers
- =
- =
- =
- =
Work Time
Divide Fractions by Whole Numbers
Solve the problems using the method of your choice.
Use one of the following strategies or one of your own.
- Visualize the problem.
- Draw a model.
- Use the fact that division is the inverse of multiplication. For example, dividing by 2 is the same as multiplying by 1 2 .
Divide a Fraction by a Whole Number
A Possible Summary
To divide a fraction by a whole number, first make a model for the fraction. You can use an area model, a bar model, a number line, or some other model.
Then divide the model into the whole number of groups. Sometimes you have to divide each fractional part of the model into smaller parts before you can divide. For example, to divide by 6, you have to divide each fourth into 2 parts to get .
To divide without using a model, you can use the inverse relationship between division and multiplication.
Formative Assessment
Summary of the Math: Divide a Fraction by a Whole Number
Write a summary about how to divide a fraction by a whole number.
Check your summary.
- Do you describe at least one way that you can use a model to divide a fraction by a whole number?
- Do you explain how to use the inverse relationship between multiplication and division to divide a fraction by a whole number?
Reflect On Your Work
Lesson Guide
Have students write a brief reflection before the end of class. Review the reflections to find out what they find confusing about dividing a fraction by a whole number.
ELL: Allow additional time for ELLs to discuss the reflection with a partner before writing to help them organize their thoughts. Allow ELLs who share the same language of origin to discuss in their language of choice and to use a dictionary (or dictionaries).
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
One thing that still confuses me about dividing a fraction by a whole number is …