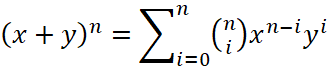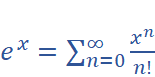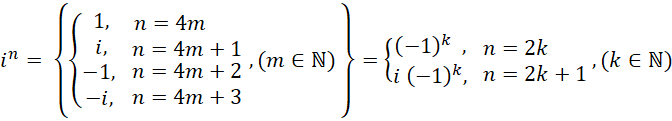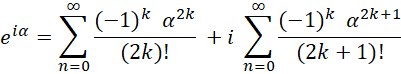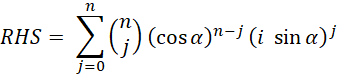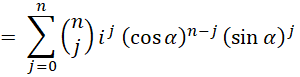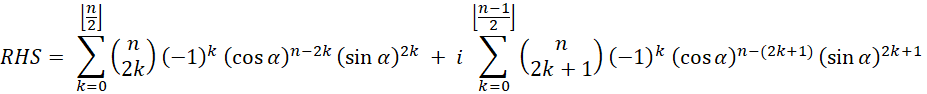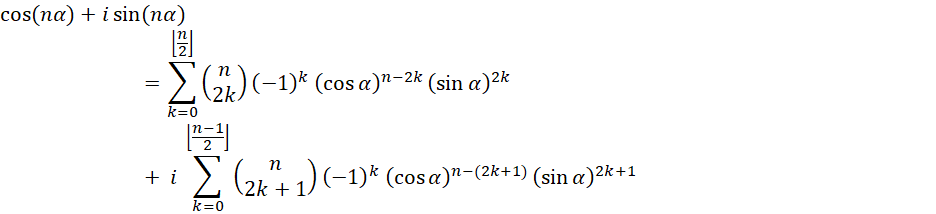Euler's Formula

Overview
Derivation of Euler's formula from a Taylor series expansion of the expontential function for a complex argument.
Derivation of the multiple angle trig identities for sine and cosine using the Binaomial theorem and Euler's formula.
(Q1) Euler's Formula from Taylor series
These notes are my attempt at learning how to create OER. Forgive the mediocre product.
Also, all these MathType MS Word formulas appear as images, hence require alt text.
Given the Taylor expansion
Derive the Taylor expansion of
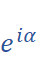 ,
, 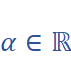
then identify its real and imaginary parts so that
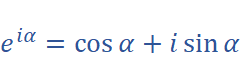 .
.
image attribution:
"Leonard Euler" by Joseph Friedrich August Darbes is licensed under CC BY 3.0 / A derivative from the original work
(QA1) Euler's Forumula derivation from a Taylor expansion
Given the Taylor expansion 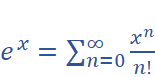 . Derive the Taylor expansion of
. Derive the Taylor expansion of 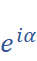 ,
, 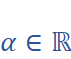 , then identify its real and imaginary parts so that
, then identify its real and imaginary parts so that
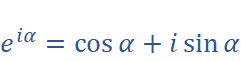 .
.
We formally extend the definition of the exponential function
to the complex domain (justification? We are happy people). Then
.
BUT, observe (and convince yourself):
Therefore,
The first series above is even (the real part) and the second (the imaginary part) is odd, and you recognize them as the Taylor series for Cosine and Sine.
Conclude:
(Euler’s Formula)
(Q2) n-tuple angle polynomial identities for sine and cosine using Euler's formula
Use the Binomial Theorem
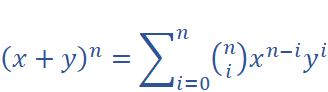 ,
, 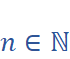
to derive a polynomial expression for
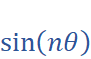 and
and 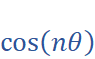
in terms of 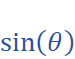 and
and 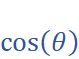 .
.
Hint: , where
.
For example, for :
.
(QA2) case n=2
Before proving the general case , let’s consider the simple cases of
, then
, to get a pattern and have a couple of examples to check our derivation in the end for the general case.
Case :
The binomial expansion takes the form
.
If , then using Euler’s formula, we have:
(eqn 2Cute)
Apply the binomial expansion to the right-hand side (RHS) above:
So eqn 2Cute takes the form:
(eqn Very 2Cute)
Equating real parts on both sides of the equation, and similarly, imaginary parts, we get our old friends, the double angle identities:
(note: both sides of identity are even functions)
and
(note: both sides of equation are odd functions)
(QA2) case n=3
Case :
The binomial expansion takes the form
.
If , then using Euler’s formula, we have:
(eqn 3Cute)
Apply the binomial expansion to the right-hand side (RHS) above:
So eqn 3Cute takes the form: (eqn Very 3Cute)
Equating real parts on both sides of the equation, and similarly, imaginary parts, we get our old friends, the double angle identities:
(even functions)
and
(odd functions)
(QA2) general case
Let’s do the general case analogously.
(eqn nCute)
Apply the binomial expansion to the right-hand side (RHS) above:
But (convince thyself)
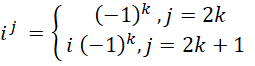
Therefore, the RHS can be separated into a real and an imaginary part as follows:
Notice the first series (the real part of RHS) above is an even function, the second series (the imaginary part of RHS) is an odd function.
Notice the upper limits of the summations. These are the Floor (in Mathematica) or Greatest Integer Function: is the greatest integer less than or equal to
. Convince yourself these are the correct limits … or prove me wrong.
Here’s an obscure hint:
(since
is an integer)
Analogously,
(since
is an integer)
So eqn nCute takes the form:
(eqn Very nCute)
Equating real parts on both sides of the equation, and similarly, imaginary parts, we get our old friends, the double angle identities:
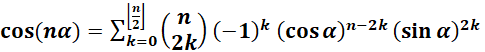
and
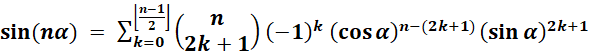
Can you provide an alternative proof, a proof by induction?
(Q3) Binomial Theorem
Use induction to derive the Binomial Theorem