WP.7.1: ADDITIONAL CENTRAL LIMIT THEOREM PROBLEMS
[WP.7.1]
I. ADDITIONAL EXERCISES
[Problem 1] Recently a professor went on a tour through one of the many local breweries. The professor is super geeky and stepped into the Quality Control Office to talk to some of the employees. He struck up a conversation with a few of the employees and found out one of the things they were checking was the operation of the bottle filling line. At the start of their shift, one of the employees randomly selected 36 bottles from the filling line during their first hour of operation. He found the average volume in the bottles from the sample was 12.10 ounces. The employees know that the equipment was set-up to run a population mean of 12.05 and a standard deviation of 0.12 ounces. Does it appear as though the brewery is over-filling the bottles or should they just continue to operate with their current settings for the rest of the shift?
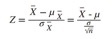
Formula for z-statistic
[Problem 2] According to a recent national study,
high school girls send 110 texts per day. Assume
the population is normally distributed with a standard deviation of 20
messages. Suppose a random sample of 40 high
school girls is studied. Answer the
following:
a. What is the probability that a selected sample is greater than 115?
b. What is the probability that a selected sample is less than 102?
c. What is the probability that a selected sample is between 102 and 115?
[Problem 3] Pentwater Pizza works to keep the size of their pizzas very consistent. However, like any other process there is variation present. They cannot make every medium pizza exactly 18 inches in diameter. The manager studied the process and found it was normally distributed with a standard deviation of 0.8inches. Based on this information answer the following:
a. What is the probability a random sample of 36 pizzas from today have a sample mean of 19+ inches?
b. What is the probability a random sample of 36 pizzas from today have a sample mean of 17.75 to 18 inches?
c. What is the lower boundary of the 90th percentile pizza size for a sample of 36 pizzas?
Solutions:
[Problem 1] Z-Value = +2.50; P(12.05<x) =0.0062
[Problem 2] a.0.0571 b.0.0057 c.0.9373
[Problem 3] a.”0” b.0.4699 c.18.171