- Author:
- Ann DeChenne, Oregon Open Learning
- Subject:
- Language Education (ESL), Geometry
- Material Type:
- Lesson, Lesson Plan
- Level:
- High School
- Tags:
- License:
- Public Domain Dedication
- Language:
- English
- Media Formats:
- Downloadable docs, Text/HTML
Education Standards
High School Right Angle Trigonometry Application Lesson
Overview
This is a lesson familiarizing students with right triangle trigonometry with applied problem solving.
LESSON DESCRIPTION
Right Triangle Trigonometry
Author of the Lesson: Ransford ‘JR’ Rogers – Math; Ann DeChenne – Emergent Bilingual Adaptation
Lesson Summary/Overview: This is a lesson familiarizing students with right triangle trigonometry with applied problem solving.
LESSON GOALS AND OBJECTIVES
Alignment and Objectives
Content Standards: CCSS.MATH.CONTENT.HSG.SRT.C.6 Understand that by similarity, side ratios in right triangles are properties of the angles in the triangle, leading to definitions of trigonometric ratios for acute angles.
CCSS.MATH.CONTENT. HSG.SRT.C.7 Explain and use the relationship between the sine and cosine of complementary angles.
CCSS.MATH.CONTENT.HSG.SRT.C.8 Use trigonometric ratios and the Pythagorean Theorem to solve right triangles in applied problems. (an extension)
Content Standards Vocabulary: Similarity, ratio, trigonometric ratio, acute, angle, sine, cosine, and complimentary.
Content Objectives: Students will be able to:
- Label sides and angles of right triangles,
- Find unknown angle measure in right triangle using sine, cosine and tangent ratios
- Interpret and solve real-life and applied problems using right triangle trigonometry.
- Draw a figure for a question and use it to find an unknown angle in a right triangle
ELP Standards: ELP 11-12.1 Construct meaning from oral presentations and literary and informational text through grade-appropriate listening, reading, and viewing.
ELP 11-12.4 Construct grade- appropriate oral and written claims, and support them with reasoning and evidence
ELP 11-12.5 Conduct research, evaluate, and communicate findings to answer questions or solve problems
ELP Standards Vocabulary: claims, evidence, reasoning, evaluate, construct meaning.
- Language (ELP) Objectives: Students will be able to construct meaning, both oral and written claims, and evaluate and communicate findings.
Supporting Academic Language
Language Functions: Explaining, Describing, Justifying, Sequencing
Language Modalities: Writing, Listening, Speaking, and Limited Reading
Vocabulary:
Academic: Right Triangle, Modeled, Depression, Horizontal, Vertical
General: Ladder, Shadow, Slide, Kite, Ramp, Leaning
Syntax or Sentence Structure(s):
Discourse: Students will work and discuss with partners.
Possible sentence starters or frames:
- The _____ of the ______ is _______
- To find the ______ of the _____ I started by _______
- The angle of_______ is looking ______ from the _____
- ______ and _____ are the ______ of the ____
LESSON PREPARATION
Considerations
Prerequisite Knowledge and Skills: Note: This is an application lesson (word heavy). Application lessons are word problems and work with real life modeling. This lesson would follow a computational lesson where students learn the numbers portion of the mathematics.
Students should be familiar with ratio & fraction; be able to solve for a missing side using right triangle trigonometry (not in application); solve for missing angle using right angle trigonometry (not in application).
Instructional Materials
Resources, Materials, and Technology required or recommended for the lesson: pictures for word wall, white board or poster paper for sentence frames or sentence starters. This is a paper pencil assignment.
Learning Supports
Accessibility: Word Wall, Vocabulary, Graphics, Notetaker, Partnering
Instructional Supports
Differentiation:
L1 (First/Dominant Language) Supports: Mathematical visual aids, mathematical and academic language visual support,
L2 (Second/Learning Language) Development (by level):
Level 1:
Listening: Demonstrating academic vocabulary with visual; Use simplified language.
Reading: Building background through pre-teaching using visuals, and picture walks; Promoting drawing, graphic organizers, sorting, labeling, copying, underlining, highlighting; All support for aforementioned level.
Speaking: promoting communication in home language (utilizing electronic translation devices); honoring “silent period” without forcing speech; speaking language aloud when writing; pre-teaching through pictures, videos, and read-aloud while when writing; supplying word bank, anchor charts, and pictures.
Writing: supplying word and picture banks; providing simple graphic organizers; allowing writing in home language.
Level 2:
Listening: offering vocabulary support through repetition, context clues, and visuals; using think pair share; issuing a note-taking template with visual support: all support for aforementioned levels.
Reading: asking comprehension questions with yes/no and simplified language response options; all support for aforementioned levels.
Speaking: providing sentence frames; all support for aforementioned levels
Writing: all support for aforementioned levels.
Level 3:
Listening: sharing academic vocabulary with increasing quantity and complexity, supported by context clues, repetition, and visuals; conduct checks for understanding; using think-pair-share or think-write-pair-share; all support for aforementioned levels
Reading: all support for aforementioned levels.
Speaking: Using think pair share; incorporating academic vocabulary in conversations with teachers and peers; all support for aforementioned levels.
Writing: all support for aforementioned levels.
Level 4:
Listening: allowing opportunities to answer open-ended or specific questions alone or with partners; all support for aforementioned levels.
Reading: all support for aforementioned levels.
Speaking: all support for aforementioned levels.
Writing: all support for aforementioned levels.
Level 5:
Listening: all support for aforementioned levels.
Reading: all support for aforementioned levels.
Speaking: all support for aforementioned levels.
Writing: all support for aforementioned levels.
LESSON PROCEDURES
Anticipatory Set/Motivation/Hook
Time: 5 Minutes
Teacher Does/Students Do:
Teacher will point out word wall/graphics (either posted on wall or printed in packet). If needed students will be given time to look up words and or translation of words and if needed to speak with a language partner. The computational lessons have already taken place. This step is to familiarize the students with the language necessary to successfully complete the word problems.
*Language learner can utilize peers, or electronic translators (smart phone, hand held, computer) to assist with meaning making.
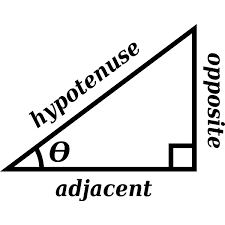
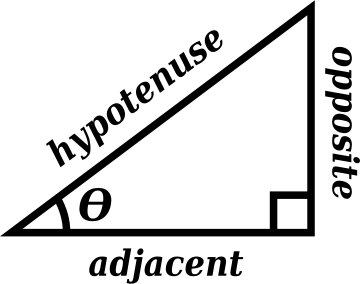
Teacher will review concepts of opposite and adjacent and how they connect to sine of hypotenuse (SOH), Cosine over Hypotenuse (COH) as well as Tangent over Adjacent (TOA). Academic vocabulary pictures will be displayed in the classroom.
Focused Instruction (Teacher-as-Model)
Time: 10 minutes
Teacher Does/Students Do:
Teacher: Will pass out guided notes to students.
Teacher: Will go over key words and concepts of Right Triangle Trigonometry and assist class with filling in the guided notes, using computer or document camera.
Students: Will follow and fill in guided notes. Guided notes to be used as a resource while solving problems.
*Guided notes provide a review of key mathematical concepts and allow for visual understanding. A diagram is included for labeling. Academic vocabulary is on display in the classroom for assistance.
Guided Instruction (Teacher-to-Student Joint Responsibility)
Time: 20-30
Teacher Does/Students Do: After going over guided notes Teacher will model problem solving with students.
Teacher will model practice problem A): A ladder leaning is what part of the right triangle.
Students will follow along with their notes.
Student will practice problem B) How Long a shadow is, is what part of the right triangle?
Students will turn to partner to Think Pair Share
Teacher follows up with students.
Teacher will model practice problem C) A bird 30 feet up in a tree is what part of the right triangle.
Students will follow along with their notes.
Student will practice problem D) A slide is modeled as what part of the right triangle?
Students will turn to a partner to Think Pair Share.
Teacher will follow up with students.
Group Application (Student-to-Student Joint Responsibility)
Time: 20-30 Minutes
Teacher Does/Students Do: See process above as students Think Pair Share sample questions. Students have the opportunity to use L1 and translanguage with other students.
Individual Learning (Independent Practice and Application)
Time: 30
Teacher Does/Students Do: Students are given worksheet with 8 practice word problem to complete. Teacher will monitor students’ progress and redirect and support as needed.
Closure
Time: 10 minutes
Teacher Does/Students Do: Teacher asks students to take out a piece of paper and to choose a problem they have completed. On the paper, students will write out the process they went through to solve the problem. Lower language learners can write exit ticket in the L1 and teacher can use technology to translate and evaluate the answer.
ASSESSMENTS
Formative Assessment
Content: Both modeling and practice questions will be used for formative assessment
Language: Students use of language during Think Pair Shares and writing practice at the end of class will be monitored as a formative assessment.
Plans for Summative Assessments
Content: Solving for side angle application situations
Language: Practiced vocabulary and sentence frame.
EXTENSIONS
Ideas for Key Assignments, Extensions, and Adaptations for Online Learning Environments: Exit out the door and/or extension. Students can write a in full and complete sentence how they solved a problem. This will access the writing domain and allow for the practice of using the vocabulary.
Attachments
Lesson plan
- review the concepts of opposite and adjacent and how they connect to SOH, CAH, TOA
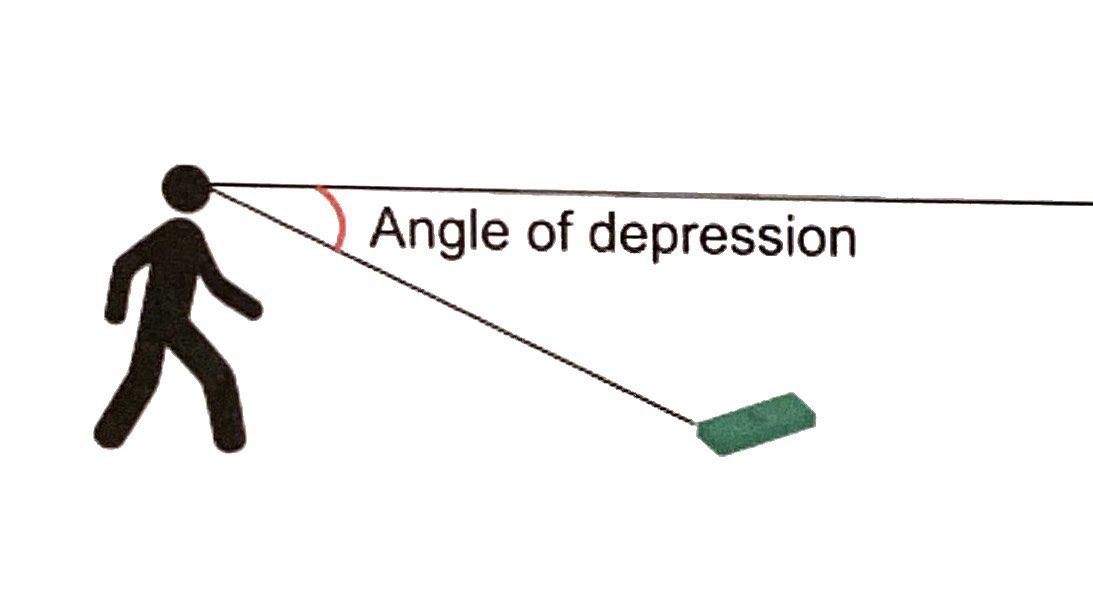
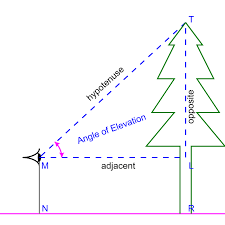
- Fill in the right triangle in the guided notes labeling the sides and the angles of elevation and depression
- Review some of the common key words and phrases and which parts of the right triangle they are modeled to.
- Check for understanding:
- A ladder leaning is what part of the right triangle
- How long s shadow is, is what part of the right triangle
- A bird 30 feet up in a tree is what part of the right triangle
- A slide is modeled as what part of the right triangle
- Do examples 1-4
- Give 8 practice questions
- Collect practice at the end of class for feedback and review.
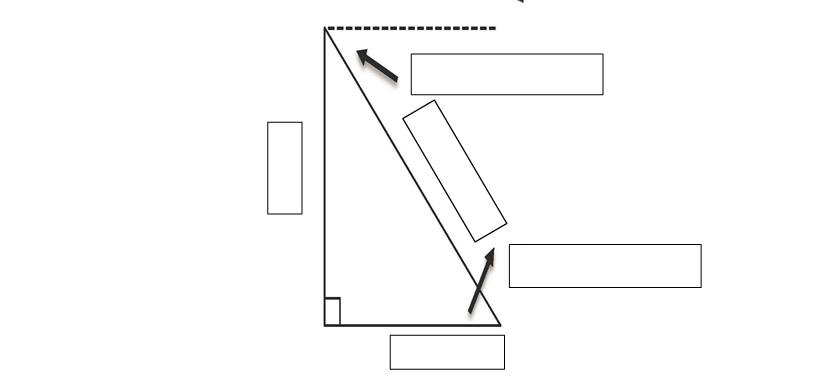
Right Triangle Trigonometry Applications Guided Notes Name_______________
Key words and phrases in application questions
- The angle of elevations is looking _______________________from the horizontal
- The angle of depression is looking _______________________from the horizontal
- “Away from or distance from an object is the ____________________ part of the triangle
- “height”, “high” or “tall” are the __________________________part of the triangle
- “Rises and “above the ground” are the _______________________________part of the triangle
- Something “leaning” is the ___________________________ of the triangle.
- Shadows are connected to the _____________________part of the triangle
- Kite strings, ladders, wires, slides and ramps are all modeled as the __________of the triangle.
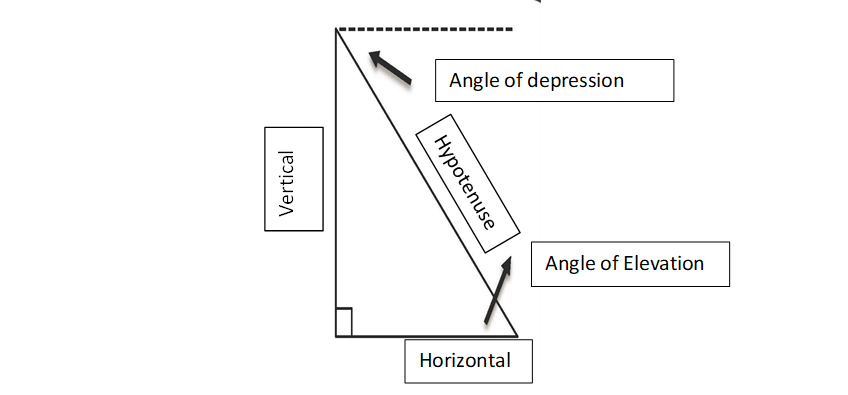
Right Triangle Trigonometry Applications Guided Notes Name_______KEY______________________
Key words and phrases in application questions
- The angle of elevations is looking _______Up_________________from the horizontal
- The angle of depression is looking ________Down________________from the horizontal
- “Away from or distance from an object is the _______Horizontal______________ part of the triangle
- “height”, “high” or “tall” are the _________Vertical__________________part of the triangle
- “Rises and “above the ground” are the _________Vertical_______________________part of the triangle
- Something “leaning” is the ______Hypotenuse______________________ of the triangle.
- Shadows are connected to the _____Horizontal___________________part of the triangle
- Kite strings, ladders, wires, slides and ramps are all modeled as the ____Hypotenuse________of the triangle.
Right Triangle Trigonometry Application Name________________________
Answer each application questions
A math student is standing 25 feet from the base of the Washington Monument. The angle of elevation from her horizontal line of sight is 87.4°. If her “eye height” is 5 ft., how tall is the monument?
A 25-foot tall flagpole casts a 42-foot shadow. What is the angle that the sun hits the flagpole?
Elise is standing on top of a 50-foot building and sees her friend, Molly. If Molly is 30 feet away from
the base of the building, what is the angle of depression from Elise to Molly?
Kristin is swimming in the ocean and notices a coral reef below her. The angle of depression is 35° and the depth of the ocean, at that point is 250 feet. How far away is she from the reef?
Standing 100 feet from the base of a building, Sam measures the angle to the top of the building from his eye height to be 50°. How tall is the building?
Over 4 miles (horizontal), a road rises 200 feet (vertical). What is the angle of elevation?
An 18-foot ladder rests against a wall. The base of the ladder is 10 feet from the wall. What angle does the ladder make with the ground?
Luke is flying a kite and realizes that 400 feet of string are out. The angle of the string with the ground is 50°. How high is Luke’s kite above the ground?
Ladder
Slide
Shadow
Kite
Ramp
Leaning
Right Triangle
Adjacent
next to

Modeled
Horizontal
Vertical
Hypotenuse