- Author:
- Ansgar Fehnker
- Subject:
- Computer Science, Information Science
- Material Type:
- Unit of Study
- Level:
- Community College / Lower Division, College / Upper Division
- Tags:
- License:
- Creative Commons Attribution Share Alike
- Language:
- English
02_3DTranslate
03_ProgramWithCamera
04a_SimpleField
04b_FieldWithObstacles
05_WalkerOnField
06_2DHideAndSeek
07_WaveSurface
08_3DWalkWithObstaclesAndLight
3D Modelling with Processing

Overview
This workshop covers the basics of 3D modelling in Processing. From the 3D coordinate system, placing different shapes, surfaces, and camera angles. This introductory workshop is suitable for all students with some basic Processing knowledge. We assume that you are familiar with 2D shapes in Processing, including pushMatrix, rotate and translate. This workshop will only cover basics, sufficient to create a landscape with 3D objects and a moving object.
Lost in Translation
We assume that you already know how to do graphics in 2D in Processing; how to set the size of a canvas, draw rectangles, and how to use pushMatrix and popMatrix in combination with translate to move the origin of the canvas to a different location on the canvas. The latter is especially important to understand for 3D because that is the main mechanism to place objects in 3D space.
Mac users should use the latest version of Processing for this tutorial.
Recap: Placement of 2D objects.
The following setup will create a canvas 400 wide and 400 high, and set the rectMode to CENTER, which means just that a rectangle is positioned by its central point (rather than the top-left corner). We assume throughout this unit that the rectMode is CENTER since it is more consistent with how 3D boxes will be placed. More on that later. First, have a look at the program and what it will create.
void setup(){ size(400,400); rectMode(CENTER); } void draw(){ background(255); fill(100); rect(0,0,100,100); }
It creates a small rectangle in the top-left corner. Since we chose rectMode(CENTER), only part of the rectangle is visible. Most of it is outside of the canvas, as the center of the rectangle is at position (0,0), the top left corner of the canvas.
The following is the common way in Processing to place a rectangle in the center of the canvas:
void setup(){ size(400,400);
rectMode(CENTER);
}
void draw(){
background(255);
fill(100);
rect(width/2,height/2,100,100);
}
size(400,400);
rectMode(CENTER);
}
void draw(){
background(255);
fill(100);
rect(width/2,height/2,100,100);
}So far so good.
Recap: Placement with translate
Another way in Processing is to place objects in a different spot is to move the origin of the canvas, i.e. to change the coordinate system. To manage changes of the coordinate system and to limit the scope of this changes, you use pushMatrix() and popMatrix() in Processing. The command pushMatrix() stores the current coordinate system, then you can manipulate it as you please, and calling popMatrix() restores the one you stored. These two usually come in blocks, starting with pushMatrix() and ending with popMatrix().
The following is a way to place a rectangle in the center of the screen (we omit the setup):
void draw(){ background(255); pushMatrix(); translate(width/2,height/2); fill(100); rect(0,0,100,100); popMatrix(); }
This does exactly the same as the previous program. Differently. The nice thing is that you can nest those blocks, for example, to put a red rectangle 200 pixels to the right of the current one. Instead of computing the new position (width/2+200), you just translate the origin 200 pixels to the right from the current position and then draw a rectangle at (0,0).
Consider the following draw() method:
void draw(){ background(255); pushMatrix(); translate(width/2,height/2); fill(100); rect(0,0,100,100); pushMatrix(); translate(200,0); fill(200,0,0); rect(0,0,100,100); popMatrix(); popMatrix(); }
Note the following:
- The second call to pushMatrix() stores the current coordinate system, i.e. that the origin is currently at (width/2,height/2).
- The second call to translate will move the origin relative to the current origin, i.e. 200 pixels to the right, of (width/2,height/2).
- The first call to popMatrix() - which matches the second call to pushMatrix() - restores the origin to (width/2,height/2).
Exercise:
Your task is to insert another pushMatrix()/popMatrix() block that puts a green rectangle 200 pixels below the grey rectangle. Insert the following code at the appropriate position:
pushMatrix(); translate(0,200); fill(0,200,0); rect(0,0,100,100); popMatrix();
You can start with the code that is attached to this section.
Into a new dimension
Now that we covered how to translate rectangles in 2D, we can continue to the third dimension. The first you will have to do is define a 3D renderer. We will be using P3D. To use it pass P3D to the call to size like this:
size(600,600,P3D);
Now you can place objects in 3 dimensions. While you cannot simply add a third coordinate to 2D shapes like rect en ellipse, you can specify a third dimension - once you specified the P3D renderer - in a call to translate. This is why the pervious section of this unit went on and on about translate. The following is the same program as from the last section, but now with 3 coordinates in calls to translate.
void draw(){ background(255); pushMatrix(); translate(width/2,height/2,0); fill(100); rect(0,0,100,100); pushMatrix(); translate(200,0,0); fill(200,0,0); rect(0,0,100,100); popMatrix(); pushMatrix(); translate(0,200,0); fill(0,200,0); rect(0,0,100,100); popMatrix(); popMatrix(); }
This does about the same as the program from the last section. So where is the third dimension? While the x-axis is horizontal, and the y-axis vertical, the third dimension the y-axis points outward from the screen.
Exercise
You can start with the code attached to this section.
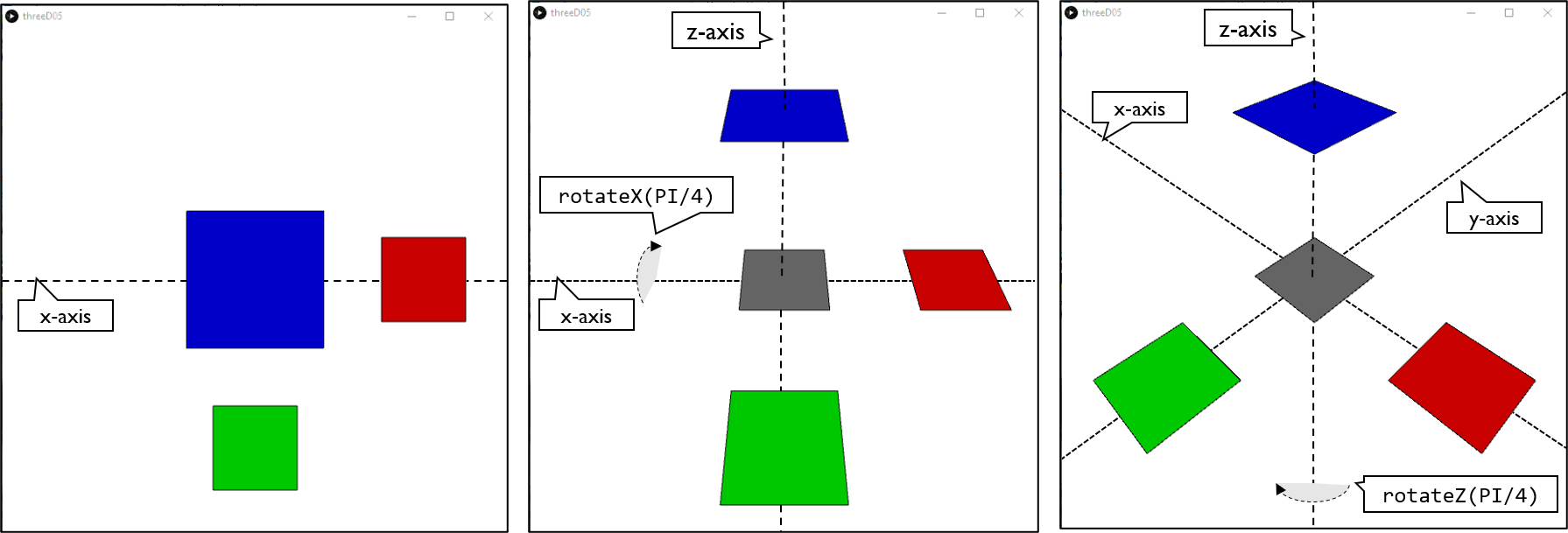
Rotations in 3D
Of course, this is not the real 3D look you might have been hoping for. To see things at an angle you have to rotate it. In 2D you can use rotate to rotate objects around the origin (which is actually a rotation around the z-axis).
In 3D we have to select which axis you want to rotate around, in addition to an angle. Consequently, there are three rotate functions, rotateX, rotateY, and rotateZ.
For example, to show the blue rectangle hovering above the grey rectangle, we can rotate the canvas around the x-axis. If you then rotate the canvas also around the z-axis you can see all three axes.
To do this, insert the rotations before you start drawing and after you have moved the origin to the appropriate point on the canvas. Suppose we change the first six lines of the draw method as follows:
void draw(){
background(255);
pushMatrix();
translate(width/2,height/2,0);
rotateX(PI/4);
rotateZ(PI/4);
fill(100);
rect(0,0,100,100);
All subsequent pushMatrix()/popMatrix() block will then be drawn relative rotations around the origin, in the middle of the grey rectangle.
Of course, 2D rectangles in 3D may not be the shapes you are looking for.
Exercise
Replace the rectangle with boxes. Simple replace any mention of rect(0,0,100,10) by box(100) to get a cube of size 100.
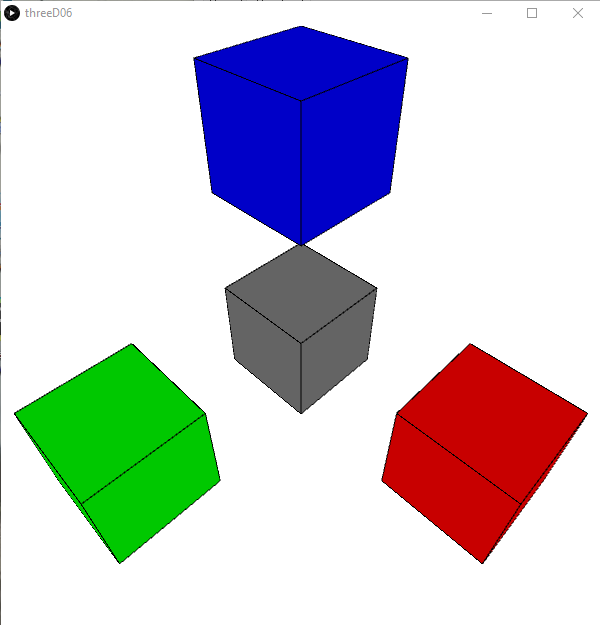
.
A point of view
You can get quite far with translating and rotating 3D objects in creating the desired look. But it is advised to use rotate and translate to place your object in 3D space and treat the point-of-view separately. From where and at what angle you view an object should not change the object (outside of quantum mechanics).
You can define the point from where you view 3D objects with the camera command. It takes three sets of three coordinates.
camera(eyeX, eyeY, eyeZ, centerX, centerY, centerZ, upX, upY, upZ)
The coordinates (eyeX, eyeY, eyeZ) defines where the camera is located, relative to the current origin. The coordinated (centerX, centerY, centerZ) define which point the camera is looking at. And the third set of coordinates (upX, upY, upZ) defines which side is up.
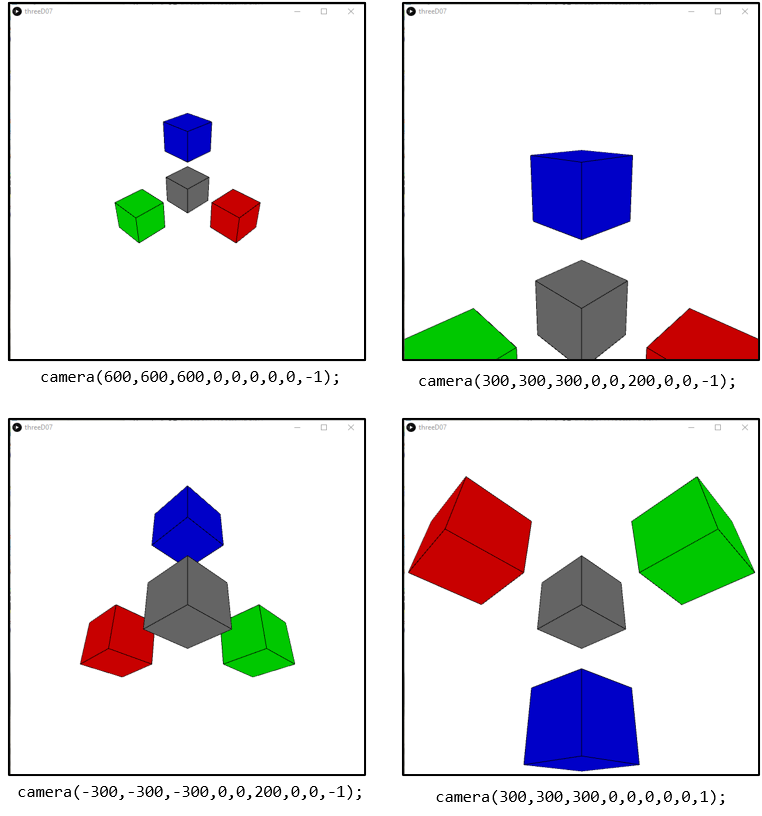
Consider the following program and the output it produces:
void draw(){ background(255); camera(300,300,300,0,0,0,0,0,-1); fill(100); box(100); pushMatrix(); translate(200,0,0); fill(200,0,0); box(100); popMatrix(); pushMatrix(); translate(0,200,0); fill(0,200,0); box(100); popMatrix(); pushMatrix(); translate(0,0,200); fill(0,0,200); box(100); popMatrix(); }
This program is also attached to this section.
Note, that this program does not start by moving the origin (width/2,height/2,0), unlike the program discussed in the previous section. It also does not use rotateX(PI/4), and rotateZ(PI/4) to get the desired view from a certain angle. This choice of what the camera looks at, from where, and at what angle is all part of the command camera(300,300,300,0,0,0,1,1,0). It puts the camera at position (300,300,300), and points it at position (0,0,0). Having those two positions is not enough to fully define the view, as you can still rotate the camera. The effect of the last set of coordinates (0,0,-1) is that the z-axis is pointing up.
Below are a few more examples of how changing the parameters of camera will change what you see.
The top-left view moves the camera to position (600,600,600), i.e further away. Consequently, the objects appear smaller. The top-right view focusses on position (0,0,200), the position of the blue box. The bottom-left view shows the same boxes at the same positions, but moves the point of view to the opposite side, to position (-300,-300,-300). And the bottom-right view changes the up-vector to (0,0,1), such that the z-axis is pointing down, instead of up. As an exercise, play with different parameters to get a feel for how the camera command works.
You can use all the 3D commands like translate, rotate, and camera to get the desired view. The rule in programming that you should write programs that confuse yourself applies especially to 3D modelling. So, to conclude this section some word of advice:
- Keep the position of your 3D separate from the view on those objects.
- Have a mental model (or a real one) of where in 3D space your objects are. Use translate and rotate in combination with pushMatrix()/popMatrix() blocks to move the objects to the desired spot.
- Treat the view on the objects separately, and use camera to achieve the desired view.
- Do not use translate, or rotate to achieve the desired view. They change the entire coordinate system.
Objects for objects
Processing is an object-oriented language. A basic rule of object-oriented programming is that objects should reflect reality, and this is especially true when it comes to 3D modelling. You shouldn't see this as a chore but as an opportunity to write well-behaved components that can be combined to form larger systems.
Challenge
The remainder of this unit on 3D modelling will create a field with obstacles,(boxes) on which keyboard-controlled walkers (spheres) can move around.
This means that we need objects that model a field, an obstacle, and a walker.
Field
As a field, we just want a square rectangle in 3D space. But instead of just drawing a green rectangle, it is better to write a class for a field that encapsulates all relevant behaviour of a field. Initially, that will not be much, but it still helps to turn a program that draws something which then resembles a field, into a model that explicitly defines what a field is.
To define a field we need to know its position, in 3D, and its size. The constructor is used to define those values and a method that displays the field. Consider the following class definition:
class Field {
float size;
float x, y,z;
Field(float x, float y, float z, float size) {
this.x = x;
this.y = y;
this.z = z;
this.size=size;
}
void display() {
rectMode(CENTER);
pushMatrix();
translate(x, y,z);
noStroke();
fill(100, 200, 150);
rect(0, 0, size, size);
popMatrix();
}
}Inside of the constructor, you see the keyword this. It is used to distinguish between the parameters, x,y,z, and size of the constructor (see Field(float x, float y, float z, float size) ) from the attributes x,y,z, and size that are defined in line 3 and 4 of this class definition. The line this.x = x means that the value of the parameter x is assigned to the attribute x. The use of this is a common idiom in languages like Processing, Java, JavaScript or Python.
The benefit of the class definition is that once we define an object of type Field, we do not have to worry about how it displays itself, just where it is and what size it is. It provides an abstraction. The following shows how to use the field in the Processing main tab:
Field playground; float fieldSize; void setup() { size(800, 800,P3D); // Pick the smaller size for the square. fieldSize = min(width, height); playground = new Field(0, 0, 0, fieldSize); } void draw() { background(200); camera(fieldSize,fieldSize,fieldSize,0,0,0,0,0,-1); playground.display(); }
The method setup() defines a square field, and the draw picks a camera angle and display the field. Note, that the position of the field itself is treated separately from the angle at which you are viewing it.
A floating green square is not exactly exciting, but in the remainder of this unit, we will extend the field class with a few additional methods, such that a Field object can work together with other objects. First, we will add a few obstacles to the field.
Obstacles
The next step is to add obstacles to the field. There are different ways to do it, but sticking by the rule that the program should reflect "reality", we take the "add obstacles to the field" quite literally. We define an obstacles class, and then add an array of obstacles to the field. Or to be more precise, to the Field class.
An obstacle is defined by its position and size, and to display it you have to draw a box. Since boxes are defined by their central point this requires the origin to be moved half the size of the box, above its coordinates. The class definition of an obstacle looks as follows:
class Obstacle {
float x, y, z;
float size;
color obstacleColor;
Obstacle(float x, float y, float z, float size) {
this.x = x;
this.y = y;
this.z = z;
this.size = size;
this.obstacleColor=color(random(0, 255), random(0, 100), random(0, 255));
}
void display() {
pushMatrix();
translate(x, y,z+size/2);
noStroke();
fill(obstacleColor);
box(size);
popMatrix();
}
}
Note that the constructor doe not just set the position and size, but also assigns a random colour to each obstacle.
You note that in the display method there is a pushMatrix()/popMatrix() block, that calls translate(x,y,z+size/2). The nice thing about putting this inside of a method of an obstacle object is that once you define it, and because you used a pushMatrix()/popMatrix() block you can now use it without thinking about the details of how the obstacle is displayed.
As mentioned before, we want to add obstacles to the field. And not to the main tab. This means we extend the class definition of Field. If done correctly, if an object of type Field is displayed, it will also display the obstacles. This, since the obstacles are "part-of" the field. Here is the new class definition of Field.
class Field { float size; float x, y, z; Obstacle[] obstacles; float obstacleScale = sqrt(2); //Found by trying Field(float x, float y, float z, float size, int numberObstacles) { this.x = x; this.y = y; this.z = z; this.size=size; this.obstacles = new Obstacle[numberObstacles]; float obstacleSize = obstacleScale*size/numberObstacles; for (int i=0; i<obstacles.length; i++) { //Pick a ranom point of the field minus half the size of the obstacle float randomX = x+random(-size/2+obstacleSize/2, size/2-obstacleSize/2); float randomY = y+random(-size/2+obstacleSize/2, size/2-obstacleSize/2); this.obstacles[i]=new Obstacle(randomX, randomY, z, obstacleSize); } } void display() { rectMode(CENTER); pushMatrix(); translate(x, y, z); noStroke(); fill(100, 200, 150); rect(0, 0, size, size); for (int i=0; i<obstacles.length; i++) { obstacles[i].display(); } popMatrix(); } }
The for-loop in the constructor selects random x and y position for the obstacles. It selects a random number between -size/2+obstacleSize/2 and -size/2+obstacleSize/2 to ensure that the obstacle fits fully on the field.
The constructor of Field has one additional parameter for the number of obstacles. This means that in the main tab you have to add one argument. The image shows a field with 10 obstacles.
Boxes as obstacles may be quite simple But nothing stops you from making the obstacles more interesting, adding a roof, or adding trees or walls. The basic idea remains the same: define a class that defines the object, and then use those objects in your 3D model.
The next section will add a walker to a field.
On the move
Until now the landscape is rather static. How do you move an object? Essentially like you did in 2D, except that your point of view may also change. To show how this works we add a walker to an empty field. And unlike in 2D where it would be common to view the scene from the top, we view the scene from the perspective of the walker. To keep things simple the walker will be just a sphere.
The description in the previous section also mentioned that the walker should be keyboard controlled. In 2D it would be obvious to use the UP, DOWN, LEFT and RIGHT button to move the object up, down, left, and right, respectively. In 3D, when you take the "first-person" perspective of the walker, it is more natural to associate UP and DOWN with moving forward and backward and left and right with turning left or right.
Note, that in this example we are actually only moving in 2 dimensions, over a field. Moving in 3D is of course also possible - like flying - but that would require more than a default keyboard control.
The Walker
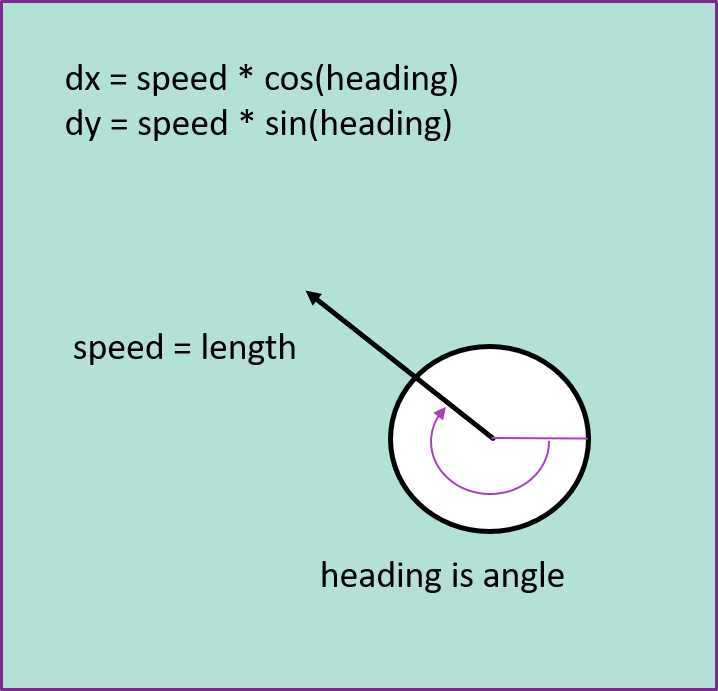
The walker is defined, just like the field and obstacles by their x, y, and z position, and their size. For a sphere that the radius. But we also need a direction, and for this unit, we decided to use a heading, i.e. an angle, from which we can compute dx and dy, the velocity in the x and y-direction. For this walker, we also want to explicitly specify the colour. The class definition of the Walker is as follows:
class Walker {
float x, y, z;
float speed;
int heading;
color teamColor;
float radius;
Field area;
Walker(Field f, float r, color c) {
area = f;
radius = r;
teamColor = c;
heading = int(random(0, 60))*6; //60 minutes of 6 degrees, makes 360 degrees.
x = area.x+random(-area.size/2+radius, area.size/2-radius);
y = area.y+random(-area.size/2+radius, area.size/2-radius);
z = area.z;
}
void view(){
float dx = cos(radians(heading));
float dy = sin(radians(heading));
camera(x-radius*dx,y-radius*dy,z+2.4*radius,x,y,z+2.4*radius,0,0,-1);
}
void display() {
pushMatrix();
translate(x, y, z+radius);
noStroke();
fill(teamColor);
sphere(radius);
popMatrix();
}
void walk() {
float newX = x + speed * cos(radians(heading));
float newY = y + speed * sin(radians(heading));
if (area.isOnField(newX, newY, radius)) {
x = newX;
y = newY;
}
}
void turnLeft() {
heading= (heading-6)%360;
}
void turnRight() {
heading= (heading+6)%360;
}
void moveForward() {
speed = radius/10;
}
void moveBackward() {
speed = -radius/10;
}
void halt() {
speed= 0;
}
}Let's have a view of the parts one by one:
- The attributes of the walker are the position, heading, speed, radius its colour, and a field. The field is not a part of the walker but exists independently. The walker is however associated with a field, meaning it can access the field, and for example, access its position.
- The constructor of the Walker requires as parameters a field, a colour, and a radius. It then selects a random initial position on the field, with a random heading.
- The method view, defines the "first-person view". The camera is situated just a bit above and behind the sphere, approximately a radius distance behind the centre of the sphere. The exact position was found by trying a few values that gave the desired effect of the top of the sphere being visible without obstructing the view.
- The display method just displays a sphere. This is intentionally independent of the view. The view may change - and it will later - but the outward appearance of the sphere remains the same regardless of who views it.
- The walk method first computes the new x and y positions, given the heading and speed, and then checks if the new position is still in the area. If it is it updates the position. This also means that we have to add a method isOnField to the class definition of Field. More on that later. The following shows how to use cos and sin to translate a heading to an increment in the x and y direction:
- The last five methods can be used to move forward, backward, turn left, right and halt. They will be used by the main tab when keyboard events happen.
As noted, the field has to provide a method to check if the walker is still on the field.
On-Field Check
The program is constructed such that the field checks if a position is on a (free) part of the field. Sure, the walker could do all of this, getting the position of the field, the size (and later where the obstacles are), but if you have to get a lot of information from another object to complete a task, it is worth considering letting that other object do the work.
For the on-field check we include the following in class Field:
boolean isOnField(float otherX, float otherY, float radius) {
float margin = size/2 - radius;
float distX = abs(x-otherX);
float distY = abs(y-otherY);
return (distX<margin) && (distY<margin);
}This method gets as parameters a position and a radius and uses a simple notion of distance.to decide if an object with that position and that radius would be on the field. If it would, it returns true.
Walking on the field
To finish this section we add the walker to the main tab of the processing program. As said, the field and the walker exists independently of another, even though you need to pass an object of type Field to the when you call the constructor of Walker.
This is the main tab followed by a short clip of the animation.
float fieldSize;
Field playground;
Walker alice;
void setup() {
size(1200, 800, P3D);
fieldSize = 3*min(width, height);// See note
playground = new Field(0, 0, 0, fieldSize);
alice = new Walker(playground, fieldSize/25, color(255, 0, 0));
}
void draw() {
background(200);
playground.display();
alice.display();
alice.walk();
alice.view();
}
void keyPressed() {
if (key==CODED) {
if (keyCode==LEFT) {
alice.turnLeft();
} else if (keyCode==RIGHT) {
alice.turnRight();
} else if (keyCode==UP) {
alice.moveForward();
} else if (keyCode==DOWN) {
alice.moveBackward();
}
}
}
void keyReleased() {
if (!keyPressed) {
alice.halt();
}
}A few notes on the program
- The main tab defines a Field called playground, and a Walker called alice. The setup() method defines objects for playground and alice. The playground is passed as a parameter to alice.
- The fieldSize is multiplied by 3 for a rather prosaic reason. If a camera is too close to a surface, in terms of the absolute number of pixels, the surface becomes transparent. In this case, this is not an effect we want, it means that we would see the red sphere. We hence scale everything by 3, the playground, and the size of alice, and the position of the camera relative to alice.
- In the draw() method you notice that it does not specify where the camera is. Instead it call method view of alice.
- The methods keyPressed() and keyReleased() control the movement of the alice.
- The method keyReleased() contains the condition if(!keyPressed) because if you control a walker by keyboard it happens that the user presses multiple buttons at once. Only releasing all buttons should stop the walker.
You can find the program attached to this section.
Hide and Seek
The exercise requires comes down to identifying which parts of the existing program can be copied where. The overall structure of the program, w.r.t the 2D version does not need to be changed. You only need to
- Add the P3D renderer to the size() in the setup()
- Remove the initial pushMarix()/popMatrix() in the main tab, together with the translate(width/2,height/2).
- Add a third coordinate to all other translates().
- Replace the rect in the Obstacle, and the ellipse and arc in the Walker by a box and sphere, respectively.
- Copy the view() method to the Walker. class.
- Call activeWalker.view() from draw().
- To improve the quality, increase the fieldSize.
As mentioned in the text, this is the main exercise, the next section are for students who managed this. Try to get the participant to this point, and treat the remainder as optional.
The last two sections did not contain any exercises. This section is in contrast one big exercise. The task is to put everything together in a game of hide-and-seek. You are given a 2D game of hide-and-seek, which might be a tad bit boring. You will see that adding the 3rd dimension makes all of a difference.
2D hide-and-seek
Attached is a 2D program of hide-andseek. It has the same components that we discussed so far, but leaves out the third dimension. This is a clip of the game:
The section will not discuss the entire 2D hide-and-seek program, but discuss some noticeable differences and additions. The program itself is attached to this section.
- The main tab defines two Walker alice an bob, and creates for each a sepate object. It also contains a variable activeWalker which is initially alice. The active walker is the walker that actually walks.
- The event hander keyPressed only changes the direction of the activeWalker. If the user pressed 'A' the activeWalker will become alice. If the user presses 'B' then it will become bob. This means by pressing 'A' or 'B' the user can switch between alice and bob.
- The method isOnField of class Field, not only checks if the other object is on the field, but also whether it is not overlapping with any of the obstacles. That is what the additional for-loop in isOnField does.
- The Obstacle class also has a method isOnObstacle, that is called by method isOnField of class Field to check for a given position and a radius whether it would overlap with the obstacle. It is similar to method isOnField, except that it checks if there is any overlap, instead of a full overlap.
- The constructor of the class Walker includes a while loop that will pick a new random starting position if the walker is not on a free spot on the field.
As an exercise try to identify and understand these parts of the program.
Exercise
This is the main exercise of the entire 3D modelling unit. Take the program of the 2D model and turn it into a 3D model, where the scene is seen from the view of the activeWalker. A few hints
- Make sure to use the P3D mode.
- Extend all translates to 3 coordinates, and replace 2D shapes by 3D shapes.
- Remove the 2D command that center the view of the screen.
- Instead use the view of the activeWalker. Of course in the 2D model, the Walker does not have a view, so you will need to add it first.
- Good luck.
If you were successful, you will see something like in this video clip:
This clip shows first the view from alice's perspective. Once the user presses "B" it will change to bob's perspective..
Making Waves
While moving in 3D on a 2D surface is interesting, it would be even more interesting if the surface weren't just a flat trectangle. The common way to achieve an uneven surface in Processing is by using so-called triangle strips.
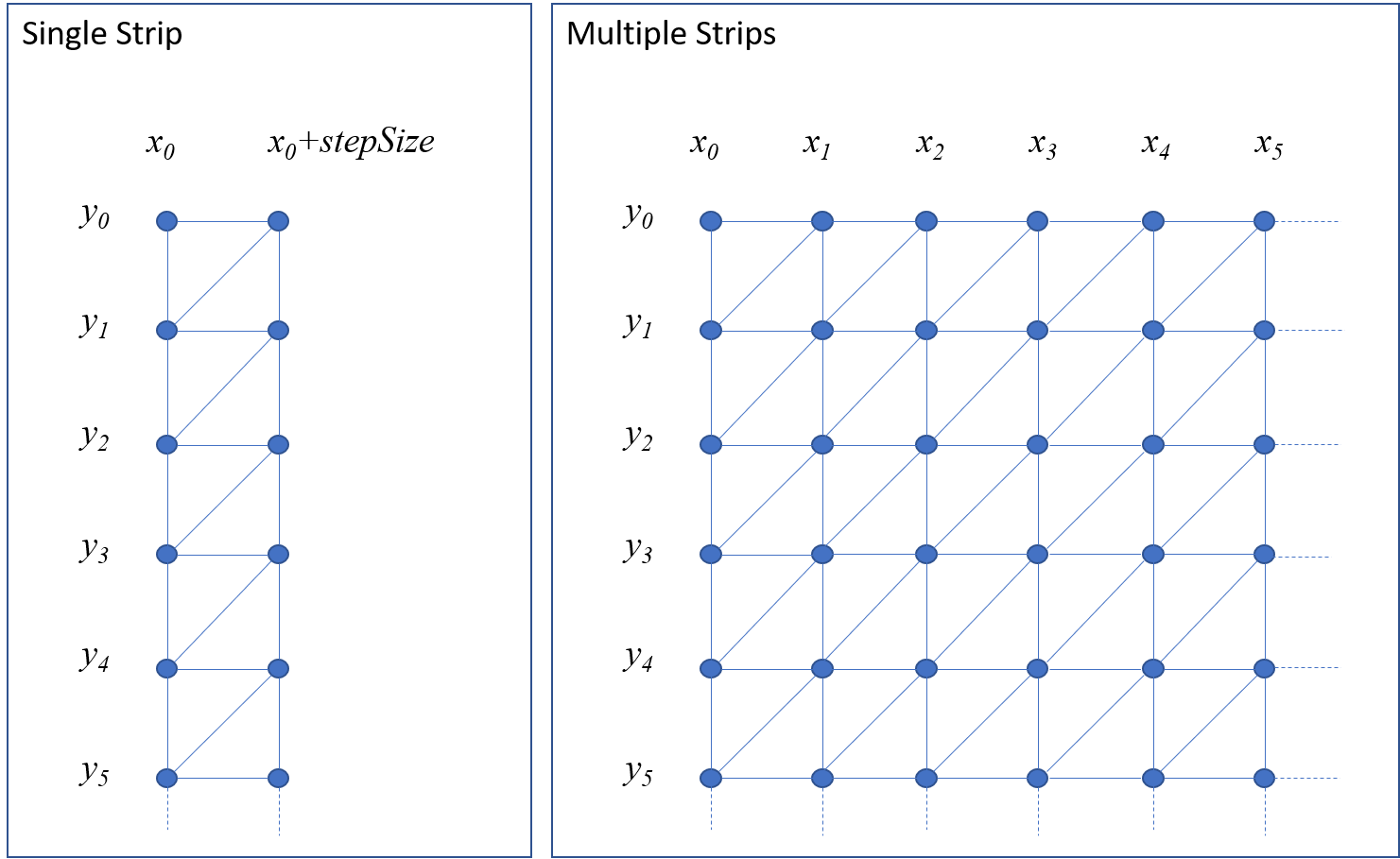
Triangle Strips
The following illustrates how a series of triangle strips creates a surface:
The following creates the simple strip:
float stepSize=20;
beginShape(TRIANGLE_STRIP);
for (float yi = 0; yi<=100; yi+=stepSize) {
vertex(x0, yi, 0);
vertex(x0+stepSize, yi, 0);
}
endShape();It creates a series of pairs of vertices, that will be connected to a triangle strip.
The next code snippet creates a series of triangle strips, which then gives you a surface:
float stepSize =20;
for (float xi = 0; xi<=100; xi+=stepSize) {
beginShape(TRIANGLE_STRIP);
for (float yi = 0; yi<=100; yi+=stepSize) {
vertex(xi, yi, 0);
vertex(xi+stepSize, yi, 0);
}
endShape();
} This gives a nice tesselation of a rectangle, but it is still a flat 2D surface. We now introduce the third dimension.
Introducing the 3rd dimension
You may notice that the third coordinate in the vertex commands were all 0, meaning that all points in the triangle mesh had the same z-value. To get an uneven surface we can define different z-values, depending on the x and y values. In this unit we are using a simple function that uses sine and cosine, but you could use other functions as well.
Since we need the z-value in different places we define the following method getZ:
float getZ(float x, float y) {
float a = 25;
float f = 2*PI*4;
return a*(sin(f*x/size)+cos(f*y/size));
}The values of a and f define the amplitude and the frequency of the wave, this means how high and how many peaks there will be.
The next step is to use getZ wherever a z-position is used. So, vertex(xi,yi,0) will become vertex(xi,yi,getZ(xi,yi)), and vertex(xi+stepSize,yi,0) will become vertex(xi+stepSize,yi,getZ(xi+stepSize,yi)).
Attached to this section you find a program that defines a class Field that will create a wave surface. Note, that an object of type field also has a z-position, but that is merely used as an offset. Given an object f of type Field, the z-position that belongs to coordinates (x,y) is f.getZ(x,y).
If you run the program it will show the following:
Exercise
Incorporate the wave-surface in the 3D hide-and-seek game. Merge the constructor and display method as they are given in the program attached to this section with the one of the 3D hide-and-seek. Then use the getZ method where you need a z-position. For example, when you create the obstacles, use getZ() rather than attribute z to place the obstacles. And in the walker use area.getZ() rather than area.z or attribute z to determine the z-position of the walker and the camera.
The following show a clip:
If you want to draw other shapes, like cyllinders, or rooftops, try some of the other shapes, like triangle fans, or quad strips.
Let there be light.
The final topic of this unit and a way to make your landscape look more realistic is to use lights. But since we got this far we leave it to you figure out the details. there are various types of light, like ambientLight() or spotLight(). you an use it to illuminate entire scenes, but also to simply illuminate a single object. And you can have multiple lights to illuminate different objects differently. And you can switch off the light by noLights().
The following shows the 3D hide-and-seek, with basic light on the surface, only.
Exercise
The final exercise is to experiment with a different type of light. Put a directional light on the walkers, or some ambient light on the obstacles. Attached to this section is a program for you start with.
This concludes this unit on 3D modelling. Have fun creating your own worlds.