- Author:
- Tom Thompson
- Subject:
- Mathematics
- Material Type:
- Activity/Lab
- Level:
- Middle School
- Tags:
- License:
- Creative Commons Attribution
- Language:
- English
- Media Formats:
- Downloadable docs
Education Standards
Bee Waggle Dance Observation Card - Gordon
Bee Waggle Dance Observation Card - Heather
Bee Waggle Dance Observation Card - Jamar
Bee Waggle Dance Observation Card - Karl
Bee Waggle Dance Observation Card - Peg
Waggle Dance Blank Observation Card
Waggle Dance Pretest
Waggle Dance Student Introduction
Proportional Reasoning and the Bee Waggle Dance

Overview
Math in Real Life (MiRL) supports the expansion of regional networks to create an environment of innovation in math teaching and learning. The focus on applied mathematics supports the natural interconnectedness of math to other disciplines while infusing relevance for students. MiRL supports a limited number of networked math learning communities that focus on developing and testing applied problems in mathematics. The networks help math teachers refine innovative teaching strategies with the guidance of regional partners and the Oregon Department of Education.
LESSON OVERVIEW
Introduction
Students will use proportional reasoning and angle measurement to analyze a hypothetical bee hive location and the related food sources visited by the bees. Using unit conversions and scaling, they will determine an average rate for the duration of the bee’s waggle dance relative to different food source distances from the hive. They will also look at how the angle of the waggle dance in the hive is related to the angle between the sun and the food source with the hive as the vertex. They will propose new hive locations and create the waggle dance observation cards that will verify the bees are using different food sources around their proposed hive.
Background for Teachers
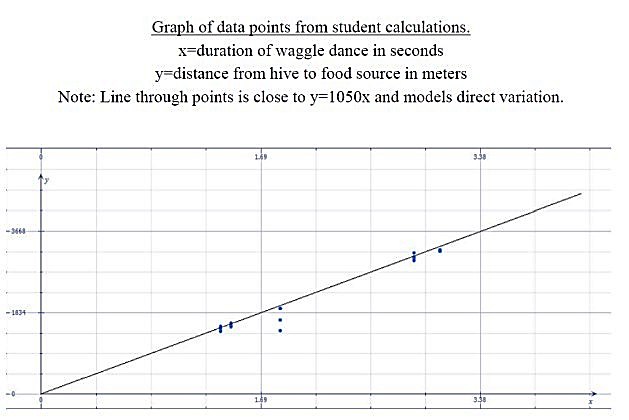
Bees perform a waggle dance in the hive to communicate the location of food sources to other bees. The waggle dance provides information about the distance of the food source and thedirection of the food source from the hive. The duration of the straight line section of the waggle dance is directly proportional to the distance of the food source. The roughly linear relationship where y=distance in meters and x=time in seconds is approximately y=1050x. The angle of the waggle dance relative to vertical in the hive replicates the angle between the food source and the sun relative to the hive as the vertex of the angle.
Note: Bees also perform two other dances for closer food sources (round dance and sickle dance) and typically do the waggle dance for distance of 150 meters or more. For simplicity, this problem will use the term waggle dance for any distance.
Core Math Concepts
Students will understand that scaling problems, unit conversion problems, and constant rate problems all can be solved using proportional reasoning.
Student Objectives
“I Can” Statements: (including extension activities)
Learning Target #1:
- I can recognize, represent, and explain proportions using tables, graphs, equations, diagrams, and verbal descriptions).
This means that:
I can determine whether two quantities represent a proportional relationship.
I can transfer my understanding of proportions to multiple real-world problems.
I can show that the waggle dance times either do or do not model direct variation.
Learning Target #2:
- I can measure and draw angles using a protractor and a ruler.
This means that:
I can measure angles between the sun and the food source from a waggle dance.
I can draw the waggle dance at the correct angle for a food source location.
Learning Target #3:
- I can use data, math concepts, and logic to determine a solution to the “Bee Problem”.
This means that:
I can use the given information and determine other information that may also be needed.
I can apply mathematical concepts and logic to determine a solution to the problem.
I can justify my claim using mathematical concepts and logic.
Materials
- Pre/Post Test
- Call to Action letter
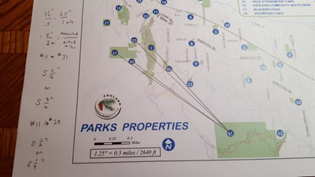
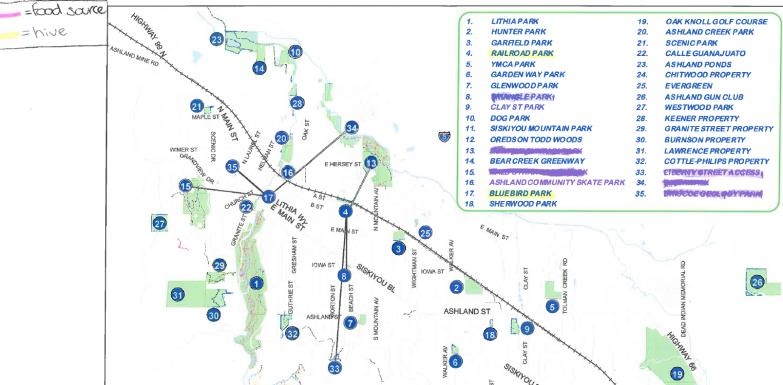
- Map of Ashland Park System (printed on 11x17 paper for correct edited scale)
- Set of five Waggle Dance Observation cards for hive at location #11
- Sun Map for 3:00 pm June 1, 2016
- Sun Map for 3:00 pm June 1,2017 (for extension) Original
- Blank Waggle Dance Observation cards
Time Required
Two 60 minute class periods.
Authors
Heather Armstrong, Jamar Boyd, Peg Hansen, Gordon Sievers
Standards
7.RP.2 Recognize and represent proportional relationships between quantities.
7.RP.2.a Decide whether two quantities are in a proportional relationship, e.g., by testing for equivalent ratios in a table or graphing on a coordinate plane and observing whether the graph is a straight line through the origin.
7.RP.2.b Identify the constant of proportionality (unit rate) in tables, graphs, equations, diagrams, and verbal descriptions of proportional relationships.
7.G.A.2 Draw (freehand, with ruler and protractor, and with technology) geometric shapes with given conditions.
Practice Standards
MP 4 - Model with mathematics
LAUNCH - SETUP
Anticipated Time
20 minutes
Suggested Grouping
Individual, Pairs, Groups, Class Discussion. This task was designed to have the students work cooperatively in groups of 2 to 4.
Teacher Questions and Actions
Give students the Call To Action Letter. Have students read it and come up with their initial questions.
Make public record of questions. If communication question does not come up, teacher should ask it.
Show Georgia Tech College of Computing video: The Waggle Dance of the Honeybee
Have a whole class discussion about the two main ideas from the video:
Summarize the two main ideas:
- The distance to a food source is proportional to the length of the waggle dance.
- The angle of the waggle dance relative to straight up in the hive corresponds to the angle between the food source and the direction of the sun.
Student Moves
Possible questions:
- Why are bees important?
- What happened to the old hive?
- Why did they not go to certain parks?
- Why are bees becoming endangered?
- Why should we worry about bees?
- Why should scientists study bees?
- How far do bees fly from their hive?
- How do bees communicate where food is?
EXPLORE - INVESTIGATE
Part 1
Anticipated Time
20 to 30 minutes
Suggested Grouping
Individual, Pairs, Groups, Class Discussion. This task was designed to have the students work cooperatively in groups of 2 to 4.
Teacher Question and Actions
Give students the map of the Ashland Park System (printed on 11x17 paper).
Have students find all the locations mentioned in the Call to Action letter. Tell the students to use the map and the information about the locations to make a conjecture about how far bees will fly from the hive.
Example #1 in Student Moves shows how students may make mistakes in how to measure the initial distance between locations. Ideally, they could measure from center to center but that is difficult to do. Some students measured from outside to outside or inside to inside of both circles giving them inaccurate measurements. Teachers should guide them towards the idea of measuring outside to inside or inside to outside to best duplicate the center to center distance.
Another common problem to watch out for is students entering fractions incorrectly in calculator. Some students would see themeasurement of \(5 \frac{7}{16}\)inches and enter 5.7 in the calculator. Have them think what 0.7 means as a fraction and compare it to \(\frac{7}{16}\).
Students might not calculate the distance exactly. Some students used equivalent fractions to get to 5 inches = 2 miles and notice that two of the measured distances are just under 5 inches and two are just over 5 inches.
Once students have the distances in miles, have class discussion about how far they think bees fly. Tell students that bees will optimally visit food sources within a two mile radius of the hive.
Student Moves
Students should use the map scale to find the distance of the locations from the hive in miles. [Converting from inches to feet to miles or from inches to miles. Possible methods include equivalent fractions, proportions, and dimensional analysis.]
Student Example #1
Students should notice that the two locations bees were spotted at are just under two miles from the hive and the two locations where bees were not seen are just over two miles from the hive. [Two miles is the typical maximum distance most bees will fly.]
Part 2
Anticipated Time
45 minutes
Suggested Grouping
Individual, Pairs, Groups, Class Discussion. This task was designed to have the students work cooperatively in groups of 2 to 4.
Teacher Question and Actions
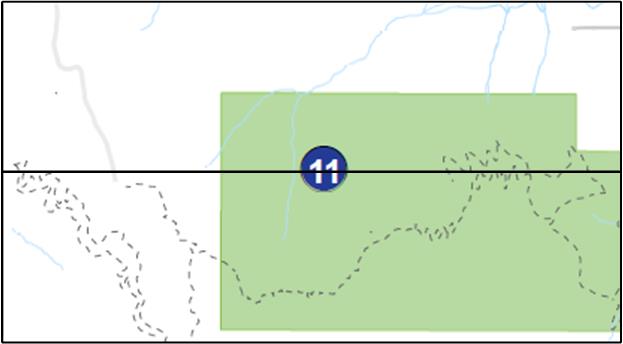
Give students the Set of five Waggle Dance Observation cards for hive at location #11 and the Sun Map for June 1, 2016.
This lesson was originally taught over 5 class periods and interpreting the relationship between the angle of the sun and the angle of the food source was difficult for many students. The process here has much more scaffolding to make the idea more accessible in a shorter time.
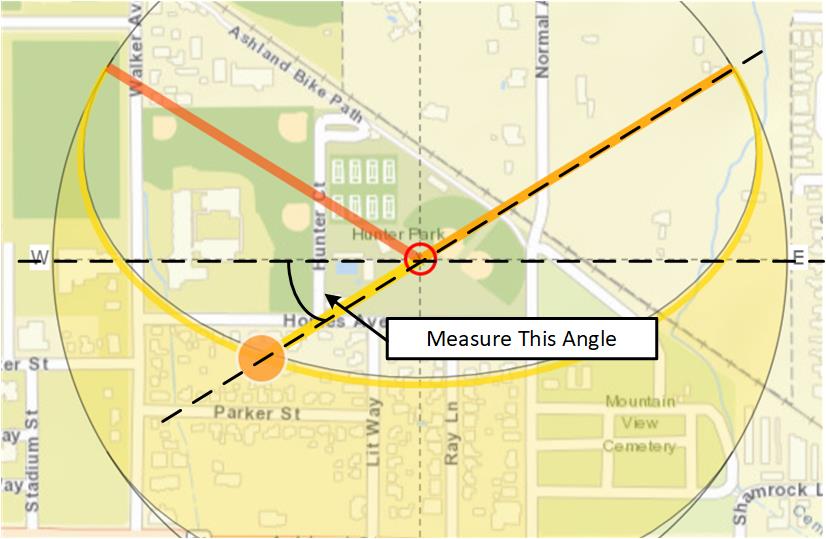
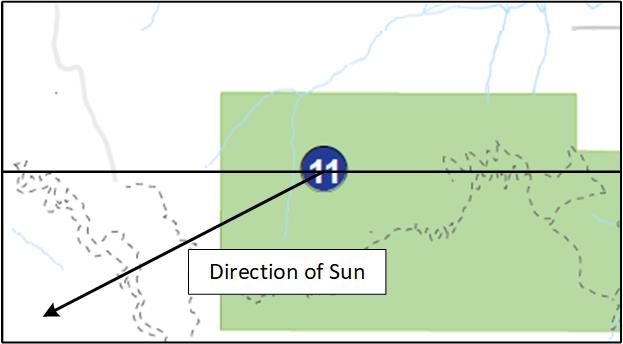
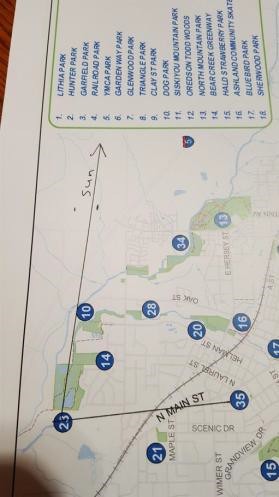
Have students draw a horizontal line through Site #11 (Siskiyou Mountain Park) on the park map similar to the horizontal line drawn through Hunter Park on the Sun Map.
Have students measure the angle down from the horizontal line to the ray going towards the sun using Hunter Park as the vertex.
Have students duplicate this angle by drawing a corresponding line on the park map using Siskiyou Mountain Park as the vertex.
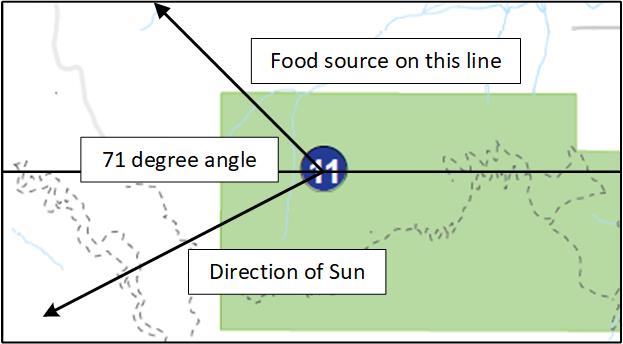
Have students use the angles from the observation cards to find the straight line path that food source is along. If measured and drawn correctly, students should be able to determine the food source that corresponds to each observation card by finding the location along each line that is within two miles of Siskiyou Mountain Park.
Watch for students using the protractor incorrectly, especially reading from the wrong scale to get the angle measurement.
Example #2 shows the map with the correct direction lines based on the observation cards.
Answer Key:
| Observer | Site |
|---|---|
| Jamar | #4 |
| Peg | #6 |
| Heather | #24 |
| Gordon | #30 |
| Karl | #33 |
Note: Observer Karl is in honor of Karl von Frisch - Nobel Prize in Physiology or Medicine (1973) – for his work on insect communication and his study of the bee waggle dance.
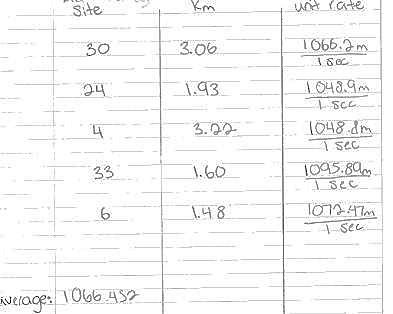
Once students have determined the matching locations for the observation cards, have them find the distance in miles and then meters between Siskiyou Mountain Park and the food source locations.
[This is to be able to relate to the roughly linear relationship for the waggle dance duration y=1050x where y=distance to food source in meters and x=waggle dance duration in seconds.]
Using the calculated distances in meters and the waggle dance duration time from the observation cards, have the students find the unit rate for each of the five observed locations in meters per second.
Have the students find the average of the five calculated unit rates. This average rate will be used to work backwards through the calculations to find the waggle dance duration if they do the extension of creating their own waggle dance cards.
This is also a way to check if students’ calculations are reasonable and to see if their measurements and calculations show the scientific relationship between distance of food source and duration of waggle dance. [If the calculations are correct, the average should be close to 1050 meters per second.] Based on slight differences in measurements, I considered numbers between 1000 and 1100 to be fairly accurate.
Example #3 shows very accurate work with students measuring and calculating correctly.
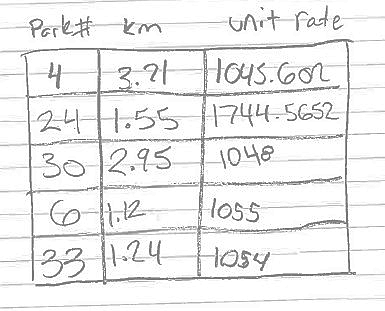
Example #4 shows that the students either measured or calculated incorrectly for Site #24 with the unit rate being 1744. This also gave them an inaccurate average of 1189. This kind of mistake often happened when a student entered an incorrect decimal in place of the fraction they measured as was mentioned earlier.
Student Moves
Draw a horizontal (East to West) line on the map through location #11
Use SunCalc to find the angle to the sun.
Draw a line on the map showing the angle of the sun.
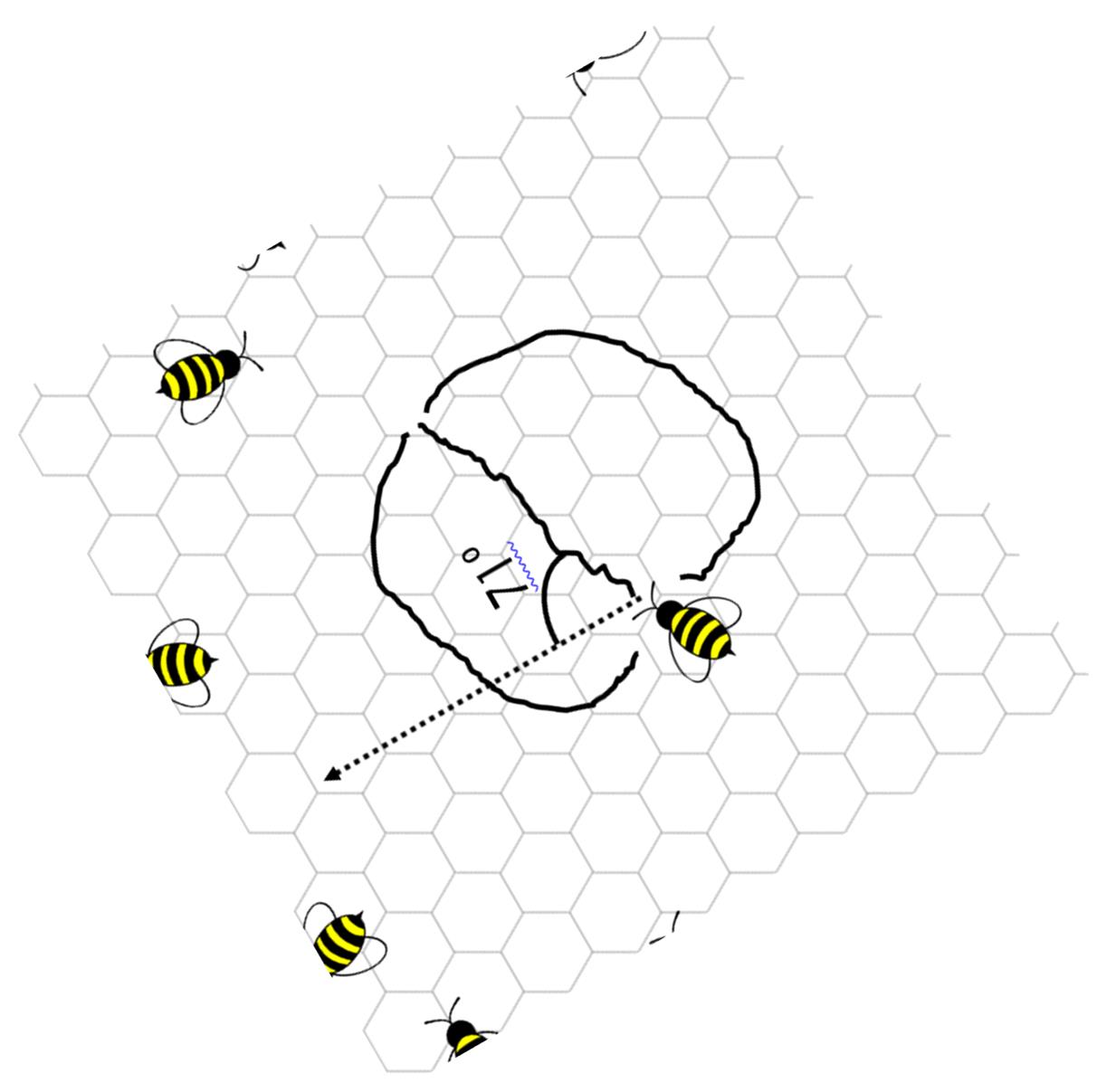
Choose one of the Waggle Dance cards to identify the angle of the bee flight. Rotating the card may help with visualization.
Draw the line of flight. In this case the card says the angle between the sun direction and line of flight is 71 degrees.
This is what the map may look like after all data is added. The arc shows the 2 mile maximum distance a bee will fly.
Students should use the map scale to find the distance of the locations from the hive in miles. [Converting from inches to feet to miles or from inches to miles. Possible methods include equivalent fractions, proportions, and dimensional analysis.]
This is similar to when students calculated the distance between the hive and food sources mentioned in the Call to Action letter.
Students should then convert from miles to kilometers using 1 mile = 1.60934 km and then multiply by 1000
Students should divide their calculated distance by the waggle dance duration for each of the five locations.
Students should average their five unit rate numbers.
Example #3
Example #4
SUMMARIZE - CLOSE
Anticipated Time
15 minutes
Suggested Grouping
Individual, Pairs, Groups, Class Discussion
Teacher Questions/Actions
Have students decide if the distances to food sources and duration of waggle dances for the five locations are proportional.
To sum up, I graphed the data from all the groups to show the nearly linear relationship that exists between food source distance and waggle dance duration.
This provided another chance to discover inaccurate results by noticing outlier data points and discussing what may have caused them.
Student Moves
Students should decide on whether the distances and times are proportional or not. [Possible methods are to compare the unit rates, compare the meters/seconds fractions, compare the meters divided by seconds as a rate of variation, make a table, make a graph showing an approximately straight line through the origin.]
Exit Tasks (Examples #5 and #6)
Give each student a blank Waggle Dance Observation card.
- Have students pick a possible hive location and a food source location within two miles.
- Have students calculate the waggle dance duration for that food source proportional to the average of the unit rates they calculated earlier.
- Have students create the observation card showing the direction of the waggle dance using the 2017 Sun Chart data.
Example #5
Hive at Site 23, Food Source at Site 35
Example #6
Waggle Dance Observation Card for Hive #23 and Food Source #35 and calculations to find waggle dance duration. The group’s average unit rate was 1052 meters per second.
Extensions
This lesson originally was taught over 5 days. These activities are beneficial for working with mathematical modeling but have been included as extensions to get the lesson completed in two days.
- Have students create several observation cards for a proposed hive site and other food source locations using the original 2016 Sun Chart data.
- Have students create several observation cards for a proposed hive site and using the sun map for June 1, 2017. They have to use a different reference direction for the sun location.
- Write a letter to the City of Ashland telling them about your proposed hive locations and why your group chose them. Explain your math and logic to justify your claim.
Examples #7 & 8 show how some students approached this part. If time had allowed, I would have had these letters looked at by a person with the Parks Department to get professional feedback on their letters.
Example #7 (Proposed hive locations and possible food sources to create observation cards)
Example #8 - Example Student Letters
References
Georgia Tech College of Computing. (2011, February 2). The Waggle Dance of the Honeybee [Video file]. Retrieved from https://www.youtube.com/watch?v=bFDGPgXtK-U