Independent & Dependent Compound Events

Overview
Students continue to extend their understanding of compound events by comparing independent and dependent events. This includes drawing the sample space to understand how the first event does or does not affect the second event. Students will solve problems with dependent compound events.
Key Concepts
Students will learn about the differences between dependent and independent events.
- Events are independent if the outcome of an event does not influence the outcome of the others.
- Events are dependent if the outcome of an event does influence the outcome of the others.
The difference can be observed by drawing a diagram to represent the sample space. For dependent events, the sample space is smaller.
Goals and Learning Objectives
- Understand the difference between independent and dependent compound events.
- Draw diagrams for dependent compound events.
- Solve compound event problems.
Number Cubes and Marbles
Lesson Guide
Have students talk with a neighbor for a few minutes about the Opening questions. They should work individually to answer them. Students do not have to complete them before starting the class discussion.
Mathematics
- Elicit from students that in the example of rolling the number cubes, the outcome of the first event does not affect the outcome of the second event. There are still 6 outcomes for each number cube, resulting in 36 total outcomes. The probability you will roll double six is . This can be seen in the now familiar table diagram:

- When drawing the marbles, once the first marble is drawn, the probability for the second marble changes. First there were 7 outcomes, but now there are 6. Each of the 7 outcomes of the first event is paired with the remaining 6 outcomes, resulting in 42 total outcomes. The probability that you will draw 2 red marbles is .
This reduction in sample space can be seen in a table diagram:

- Students are looking at independent events compared to dependent events. Independent events are not affected by each other, whereas dependent events are affected.
Opening
Number Cubes and Marbles
Look at these three problems and consider the following:
You roll 2 number cubes. What is the probability that you will roll double 6s?
You draw 2 marbles from this bag. What is the probability that you will draw two red marbles?
What is different about these two multistage experiments and compound events?


Independent Events
Lesson Guide
For the marble problem, these events are called dependent events because the outcome of one event affects the other. So far, we have only looked at independent events.
It is important to discuss that if an ace is drawn and not replaced, then the probability of drawing another ace would be .
ELL: When introducing new words like independent events and dependent events, repeat the new words at a slower pace, and write them down. Ask some of the students to repeat after you and/or work on pronunciation in small groups. Be sure ELLs feel comfortable with the pronunciation. Additionally, allow ELLs to use a dictionary.
Opening
Independent Events
Discuss the following with your classmates.
- Two events are said to be independent if the outcome of one event does not influence the outcome of the other event.
- Two events are said to be dependent if the outcome of the one event does influence the outcome of the second event.
- An example of a dependent event is if you draw an ace from a deck of cards and do not replace it. After drawing the ace, the deck has one less ace than it did before. Thus, the probability of drawing an ace on the second try has been affected by the outcome of first event.


Math Mission
Lesson Guide
Discuss the Math Mission. Students will draw a diagram to determine the probability of dependent compound events.
Opening
Draw a diagram to determine the probability of dependent compound events.
Independent or Dependent Events
Lesson Guide
Students should work with a partner during Work Time.
Encourage students to draw diagrams to understand if one event affects the sample space of another event. Look for different diagrams, both correct and incorrect, to share during Ways of Thinking to demonstrate both dependent and independent events.
Interventions
Student is not clear about independent vs. dependent events.
- Is the second outcome affected by what happens for the first outcome?
- Can you draw a diagram to represent the sample space? What does the diagram tell you?
Answers
Explanations will vary. Answers and possible explanations:
- Dependent. When drawing the first piece of fruit, the sample space is 16 pieces. When drawing the second piece, the sample space is reduced by 1.
- Independent. Tossing a coin and rolling a number cube do not affect each other. The coin toss will always have two outcomes and rolling a number cube will always have six.
- Dependent. The sample space for the second draw is one less because of the first draw.
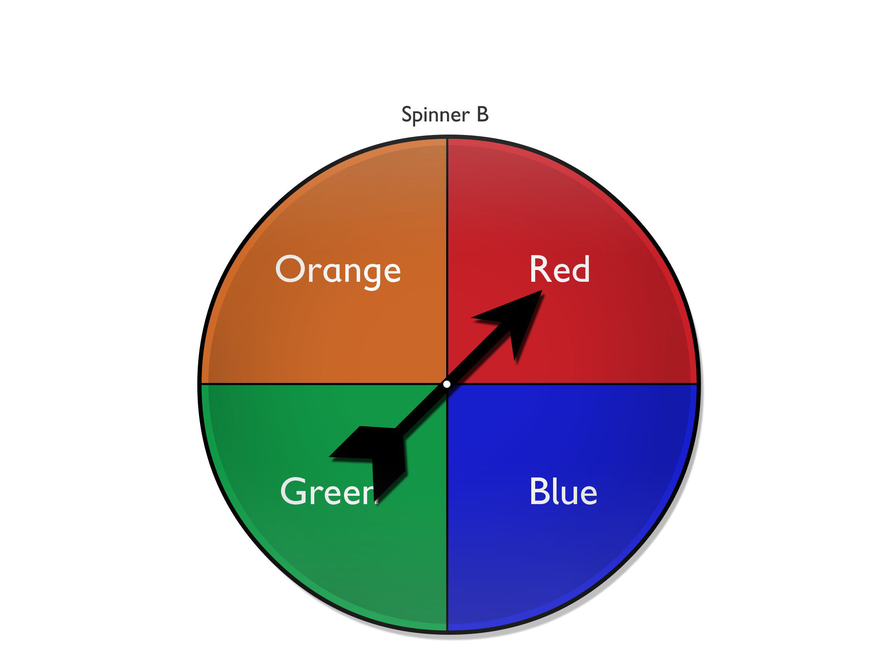
- Independent. The sample space for both spins has 20 outcomes.
- Independent. The sample space for both spins has 4 outcomes.
Work Time
Independent or Dependent Events
Which of the following events are independent and which are dependent? Explain your answer.
- There are 4 oranges and 12 apples in a bowl. You reach in and randomly take a piece of fruit to eat. Then you randomly get another piece of fruit.
- You toss a coin and roll a number cube.
- You reach into your drawer and pull out one sock. You reach in again and pull out the same color sock.
- You spin spinner A twice. You want to spin an even number and then an odd number.
- You spin spinner B twice. You want to get the same color both times.

Counters
Lesson Guide
Students should work with a partner during Work Time.
Encourage students to draw diagrams to understand if one event affects the sample space of another event. Look for different diagrams, both correct and incorrect, to share during Ways of Thinking to demonstrate dependence and independence.
Look for different strategies that students use for the four counters problems. Some may use a tree diagram or a table, while others may not need to.
Interventions
Student has an incorrect solution.
- How many outcomes are there for each event?
- Did you pair each of the first outcomes with each of the second outcomes?
- How many outcomes are favorable?
Answers
- There are four outcomes in the sample space.
- P(5) =
The probability of drawing the 5 is = 0.25 = 25% . - There would be three outcomes remaining in the sample space if you did not replace the 5.
- P(6) =
The probability of drawing the 6 when the 5 is not replaced is = = %. - Tree diagram:
 List:
List:- 5, 6
- 5, 7
- 5, 8
- 6, 5
- 6, 7
- 6, 8
- 7, 5
- 7, 6
- 7, 8
- 8, 5
- 8, 6
- 8, 7
Table: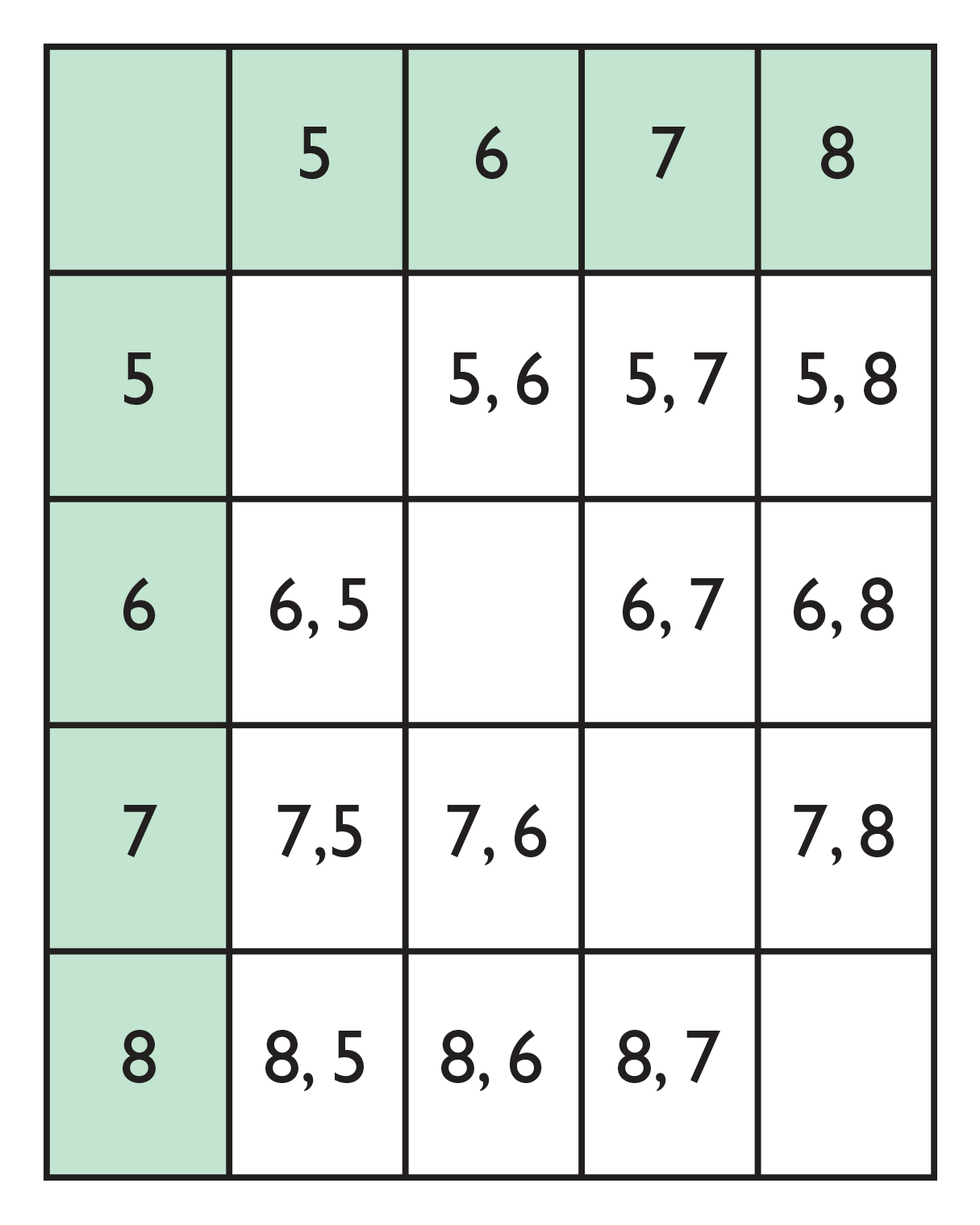
P(5, then 6) = ⋅ =
- The probability of first drawing the 5 followed by drawing the 6, if you do not replace the 5, is 1 out of 12.
Work Time
Counters
You have a box containing four counters numbered 5, 6, 7, and 8. You randomly choose one counter.
- How many outcomes are there in the sample space?
- What is the probability that you will select the 5?
- If you select the 5 and do not replace it, how many outcomes will there be in the new sample space?
- Based on this new sample space, what is the probability of selecting a 6?
- Illustrate your thinking with a tree diagram, a list, and/or a table.
- What is the probability of first selecting the 5 and then selecting the 6, assuming that you do not replace the first counter?

Marbles
Lesson Guide
Students should work with a partner.
Encourage students to draw diagrams to understand if one event affects the sample space of another event. Look for different diagrams, both correct and incorrect, to share during Ways of Thinking to demonstrate dependence and independence.
Look for different strategies that students use for the five marbles problems. Some may use a tree diagram or a table, while others may not need to.
Interventions
Student has an incorrect solution.
- How many outcomes are there for each event?
- Did you pair each of the first outcomes with each of the second outcomes?
- How many outcomes are favorable?
Answers
- Answers will vary. Tree diagram:
 List:
List:- B1, B2
- B1, R1
- B1, R2
- B1, R3
- B2, B1
- B2, R1
- B2, R2
- B2, R3
- R1, B1
- R1, B2
- R1, R2
- R1, R3
- R2, B1
- R2, B2
- R2, R1
- R2, R3
- R3, B1
- R3, B2
- R3, R1
- R3, R2
Table:
- P(red, then blue) = = = 0.3 = 30%
Challenge Problem
Answers
- Explanations will vary. Answer with possible explanation: You can form the number 63 by drawing a 3 and then a 6, or drawing a 6 and then a 3. This means there are two favorable outcomes. One way to calculate the sample space is to draw a table:
 There are 90 outcomes, so: P(forming 63) = P(drawing 6, then 3) + P(drawing 3, then 6) = = = = %
There are 90 outcomes, so: P(forming 63) = P(drawing 6, then 3) + P(drawing 3, then 6) = = = = %
Work Time
Marbles
You have a bag of 3 red marbles and 2 blue marbles. You draw 1 marble without replacing it and then draw a second marble.
- Show the sample space using a tree diagram, a list, and/or a table.
- What is the probability that you will draw a red marble and then a blue marble?

Challenge Problem
You have 10 cards numbered 0–9, lying face down. If you draw 2 cards to form a two-digit number, and you do not replace the first card, what is the probability that you will form the number 63?
- Explain your method for solving this problem.
Make Connections
Lesson Guide
During the class discussion, have selected students present their diagrams and strategies for each of the problems.
SWD: As students present their solutions, make connections between different solutions to the same problem. This allows students to see the multiple ways to solve/analyze a problem. Write down important connections, and have students copy information into their notebook.
Mathematics
Discuss the first problem, determining dependence and independence:
- Which events are independent? Why?
- Which events are dependent? Why?
Discuss the counters problem and the marbles problem:
- How is the sample space different for a dependent event compared to an independent event?
- What is the probability of drawing a blue marble and then another blue marble? How does the probability change if the events are independent (i.e., return the first marble to the bag)?
- What is the probability of drawing a 5, then drawing a 6 if you put the 5 back? How does the probability change if the events are dependent?
If any students did the Challenge Problem, have them present their methods and encourage the rest of the class to ask questions.
Mathematical Practices
Mathematical Practice 6: Attend to precision.
- Students must take care in using appropriate mathematical language to discern between the two types of compound events.
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates’ diagrams and solutions.
As your classmates present, ask questions such as:
- How did you decide which events are independent events and which are dependent events?
- How does your representation of the sample space for dependent events differ from your representation of independent events?
- How would the probability differ if the two selections were independent versus dependent?
Independent and Dependent Compound Events
A Possible Summary
Compound events can be independent or dependent. Dependent events are affected by other events. The order of events will affect the probability of a dependent event, but not an independent event. An example of an independent event is drawing a card from a deck, returning the card, then drawing a second card. An example of a dependent event is drawing a card from a deck, then drawing a second card without replacing the first one. The sample space for dependent events is smaller than that for independent events, so the probabilities are different.
SWD: Check to make sure that all students have this information in their notes. It may be helpful to provide some students with certain things to listen for during this portion of instruction. Some students may need copies of the notes from this portion of the lesson.
Formative Assessment
Summary of the Math: Independent and Dependent Compound Events
Write a summary about independent and dependent compound events.
Check your summary:
- Do you define independent events and give an example?
- Do you define dependent events and give an example?
- Do you explain how finding the probability of independent events differs from finding the probability of dependent events?
Reflect on Your Work
Lesson Guide
Have students write a brief reflection before the end of the class. Review the reflections to find out how students describe independent and dependent events.
ELL: Assess their understanding of independent events and dependent events. Ask students to write the definitions of the two terms in their own words. Assess both mathematical understanding and language. Provide students with wait time and acknowledge student responses, both verbally and with gestures.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
I would describe the difference between independent events and dependent events as…