Pre-Assessment

Overview
Students solve for missing angle measures by applying what they have learned about types of angles and the angle measures of polygons. Students do a pre-assessment at the end of the lesson.
Key Concepts
There are many defining characteristics for angles, triangles, quadrilaterals, and polygons. Students have discovered these properties throughout this unit and have investigated why they are true. These characteristics and properties will be looked at more formally in high school geometry.
Goals and Learning Objectives
- Solve for missing angle measures in polygons.
Angles in a Triangle
Lesson Guide
After students view the opening figure, have them discuss the following questions:
- What do you know about the angles in this triangle?
- Can you use what you know to solve for x?
SWD: Help students with disabilities make connections between what they have learned in previous tasks about the interior angle sum of a triangle and writing algebraic equations.
Mathematics
Students should notice the following:
- The sum of the measures of the angles of the triangle is 180°.
- The angle measures are 30°, 60°, and 90°.
Therefore:
2x = 60°
3x = 90°
Opening
Angles in a Triangle
Look at this triangle.
- What do you know about the angles in this triangle?
- Can you use what you know to solve for x?

Math Mission
Lesson Guide
Discuss the Math Mission. Students will use their knowledge of geometric figures to determine missing angle measures in polygons.
Opening
Use your knowledge of geometric figures to determine missing angle measures in polygons.
Find Angles of a Parallelogram
Lesson Guide
Monitor students as they work, asking questions to guide them if they need assistance.
SWD: Students with disabilities may take longer to develop a solid understanding of newly introduced skills and concepts. Provide direct instruction and guided practice with the skills and concepts relating to interior angle sums. Assess their understanding of newly introduced concepts, plan a review, and reinforce skills as needed.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
- Throughout the activities, students problem solve, make conjectures, and apply what they know.
Interventions
Student has difficulty getting started.
- What do you know about the angles in a parallelogram?
Possible Answers
- The measure of ∠a and ∠c is 30°. The measure of ∠b is 150°.
- In a parallelogram, opposite angles are congruent and consecutive angles are supplementary.
Work Time
Find Angles of a Parallelogram
This quadrilateral is a parallelogram.
- What are the measures of ∠a, ∠b, and ∠c?
- Explain how you determined each angle measure.

Hint:
- What is the sum of the angles in a parallelogram?
- What do you know about opposite angles in a parallelogram?
Find Angles of a Triangle
Mathematical Practices
Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.
- Notice students who justify their thinking. During the activity, students will be constructing viable arguments to explain their reasoning.
Interventions
Student has difficulty getting started.
- What is the angle sum in a triangle?
- What is true of vertical angles and supplementary angles?
Student has a solution.
- Can you explain how you solved the problem?
- Is there another way to solve it?
Possible Answers
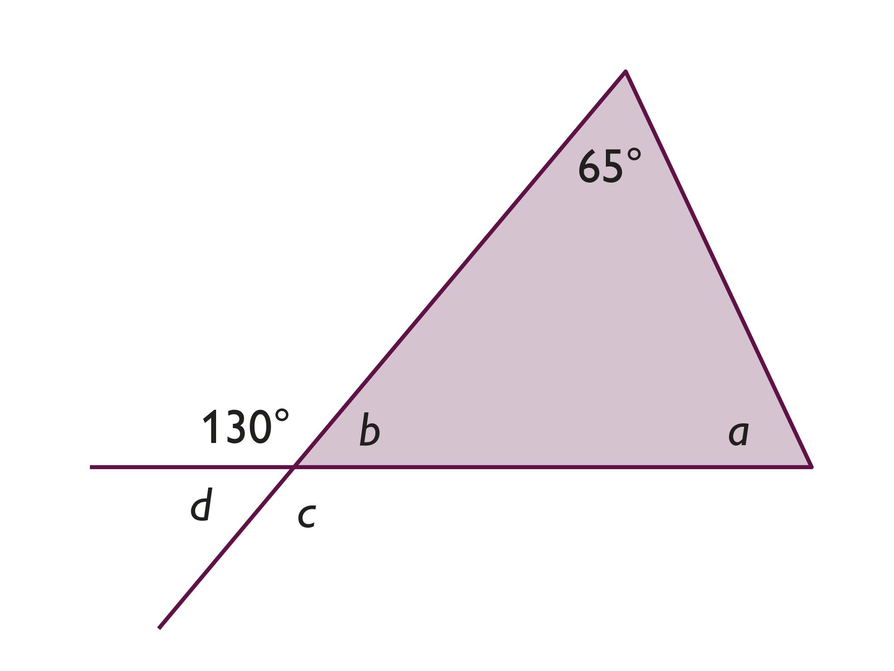
- The measure of angle a is 65°. The measure of angle b is 50°. The measure of angle c is 130°. The measure of angle d is 50°.
- Angle c is vertical and congruent to the 130° angle. Angles b and d are supplementary to the 130° angle. Angle a is 65° and can be found by adding angle b and the 65° angle, then subtracting the total from 180° (angle sum of a triangle).
Work Time
Angles of a Triangle
- What are the measures of ∠a, ∠b, ∠c, and ∠d?
- Explain how you determined each angle measure.
Hint:
- What do you know about vertical angles?
- What do you know about supplementary angles?
- What do you know about the sum of the angles in a triangle?
Find Angles of a Right Triangle
Mathematical Practices
Mathematical Practice 8: Look for and express regularity in repeated reasoning.
- Students apply the knowledge they have gained about types of angles and measures of the angles of polygons.
Interventions
Student has difficulty getting started.
- What is the angle sum in a triangle?
Student cannot solve for x.
- What is the sum of the x-variables? How many x-variables are there?
- What total number of degrees do those x-variables represent?
Possible Answers
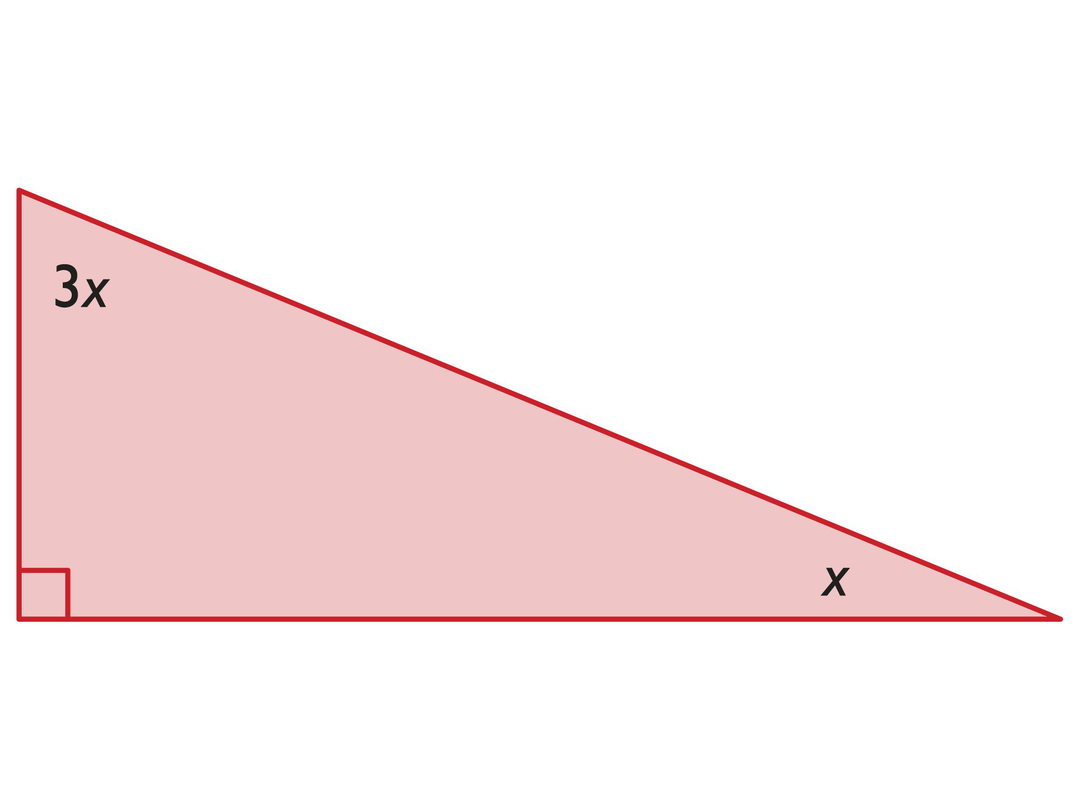
- x = 22.5°
- In a right triangle, the two non-right angles are complementary.
3x + x = 90°
4x = 90°x = 22.5°
Work Time
Angles of a Right Triangle
- Solve for x.
- Explain how you solved for x.
Hint:
- What do you know about the sum of the angles in a triangle?
- What do you know about ∠ a ?
Find Missing Angle Measures
Interventions
Student has difficulty getting started.
- What do you know about the angles in a parallelogram?
- What is the angle sum in a quadrilateral?
Student has a solution.
- Can you explain how you solved the problem?
- Is there another way to solve it?
Possible Answers
- x = 20°
- Solutions will vary. Possible solutions: A rhombus is a parallelogram, so opposite angles are congruent: 7x = 140°x = 20°. Since a rhombus has congruent sides, an isosceles triangle is formed with congruent base angles.
x + 7x + x = 180°
9x = 180°
x = 20°
Work Time
Find Missing Angle Measures
This quadrilateral is a rhombus.
- Solve for x.
- Explain how you solved for x.

Hint:
- What do you know about the angles in a rhombus?
- What kind of triangle is △ ABC ? What do you know about the angles in this type of triangle?
Find Angles in a Pentagon
Interventions
Student has difficulty getting started.
- What is the angle sum in a pentagon?
Student cannot solve for x.
- What is the sum of the x-variables; how many x-variables are there?
- What total number of degrees do those x-variables represent?
Possible Answers
- x = 120°
- A pentagon has an angle sum of 540°. The sum of the measures of two right angles is 180° (90° + 90° = 180°). Since a pentagon has an angle sum of 540°, the sum of the measures of the other three angles must be 360° (540° − 180° = 360°).
x + x + x = 360°
(teacher preference) 3x = 360°
x = 120°
Work Time
Find Angles in a Pentagon
- Solve for x.
- Explain how you solved for x.

Hint:
- What do you know about the angles in a pentagon?
- If all of the angles are x degrees, what do you know about the angles?
Find Angles in the Figure
Interventions
Student has difficulty getting started.
- What is the angle sum in a triangle? A pentagon?
- How can you find the measure of an angle in a regular pentagon?
Possible Answers
- The measure of angle a is 36°. The measure of angle b is 72°. The measure of angle c is 72°.
- Since this is a regular pentagon, the angle sum is 540°, and each angle of the pentagon measures 108°. Each of the side triangles are isosceles because two sides are congruent, so the base angles are congruent and each measures 36° (180° − 108° = 72°, 72° ÷ 2 = 36°). The sum of the measures of angle b and one of the 36° angles is 108° (108° − 36° = 72°) and angle b measures 72°. Similarly, angle c measures 72°. This leaves 36° for angle a since 72° + 72° + 36° = 180°.
Work Time
Find Angles in the Figure
This figure is a regular pentagon.
- What are the measures of ∠a, ∠b, and ∠c?
- Explain how you determined each angle measure.

Hint:
What do you know about the angles in a regular pentagon?
Prepare a Presentation
Preparing for Ways of Thinking
Look for these types of responses to share during the Ways of Thinking discussion. Look for students who:
- Use different methods to solve for the angle measures.
- Understand the Challenge Problem and can explain how they solved it, perhaps by drawing the diagonals first.
Challenge Problem
Answers
- The figure is a kite, which will be explored further in the Gallery.

Work Time
Prepare a Presentation
- Select two of the previous problems: the one you had the most difficulty with, and the one that was easiest for you. Prepare a presentation about your solutions.
- Be prepared to explain and justify each step of your solutions.
Challenge Problem
- Imagine a quadrilateral that has two pairs of congruent sides with diagonals that are perpendicular to each other. However, the quadrilateral is not a rhombus. Can you draw this figure?
Make Connections
Mathematics
Facilitate the discussion to help students understand the mathematics of the lesson. Ask questions such as the following:
- What “tools” did you use to solve each of problems?
- How did you decide what to do first in order to solve the problem?
- How did the definitions and characteristics of different figures help you?
- How did the properties of angle measures help you?
- What method can you use to find the angle sum of any polygon?
- What do you know about the angles in a parallelogram?
- What is true about vertical angles and supplementary angles?
- How was the mathematics represented differently by [students]? What was the same? What was different?
- How did [students] make sense of the problem?
- Can you state what [students] said in a different way?
ELL: When selecting a group of students to present during the “Ways of Thinking” section, ensure students present a topic they are confident about. Have students draw diagrams or demonstrate their knowledge in some other way than through verbal language alone.
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates' strategies and explanations for finding the missing angle measures.
Hint:
As your classmates present, ask questions such as:
- What do you know about the angles in a parallelogram?
- What is the sum of the angles in a triangle/quadrilateral/pentagon?
- What is true about vertical angles and supplementary angles?
- How did you decide what to do first in order to solve the problem?
- Is there another way to solve the problem?
- What total number of degrees do the x -values represent?
Angles in Polygons
A Possible Summary
The properties of vertical, supplementary, adjacent, and complementary angles all play a part in describing geometric figures. Some of the characteristics that describe triangles and quadrilaterals, including how their angles are related to each other, are based on these types of angles. Using this information, you can find the measures of missing angles.
Formative Assessment
Summary of the Math: Angles in Polygons
Write a summary about finding missing angle measures in polygons.
Hint:
Check your summary:
- Do you explain how you can use the relationships of angles in different types of polygons to find missing angles?
- Do you describe some things you know about the angles in different types of polygons?
Analyzing a Hexagon
Lesson Guide
This task allows you to assess students’ work and determine what difficulties they are having. The results of the Self Check will help you determine which students should work on the Gallery and which students would benefit from review before the assessment. Have students work on the Self Check individually.
Assessment
Have students submit their work to you. Make notes on what their work reveals about their current levels of understanding and their different problem-solving approaches.
Do not score students’ work. Share with each student the most appropriate Interventions to guide their thought process. Also note students with a particular issue so that you can work with them in the Putting It Together lesson that follows.
Interventions
Check questions that are related to this work.
Student does not calculate m∠1 correctly.
- What is the sum of the angle measures in a triangle?
- What is the sum of the angle measures that you know?
Student does not calculate m∠2 correctly.
- How can you find the measure of ∠FGE?
- What is the sum of the angle measures in a triangle?
Student does not see that ∠3 and ∠BGC (27°) are supplementary angles.
- What type of angle do ∠BGC and ∠CGE form?
Student provides a poor explanation, such as explaining calculations rather than giving mathematical reasons.
- What is the sum of the angle measures in a triangle?
- What do you know about the angles formed by two intersecting lines?
Student provides adequate solution to all questions
- Find a different way of solving the problem.
Possible Answers
The measure of ∠1 is 63°.
The measure of ∠2 is 135°.
The measure of ∠3 is 153°.
The measure of ∠4 is 45°.
The measure of ∠5 is 27°.- Solutions will vary. Students may use the following concepts to find the angle measures:
• Complementary angles to find m∠1
27° + m∠1 = 90°
m∠1 = 63°
• The angle sum of a triangle is 180° to find m∠2 (and m∠1).
18° + 27° + m∠2 = 180°
m∠2 = 135°
• Supplementary angles to find m∠3
27° + m∠3 = 180°
m∠3 = 153°
• Consecutive angles of a parallelogram are supplementary to find m∠4.
m∠2 + m∠4 = 180°
135° + m∠4 = 180°
m∠4 = 45°
• Opposite angles of a parallelogram are congruent to find m∠5.
18° + m∠5 = m∠4
18° + m∠5 = 45°
m∠5 = 27°
- The sum of the angles in the hexagon is 720°. There are 6 sides, so use the general rule:
s = (6 − 2)180°
s = 4⋅180°
s= 720°
Students could also add together the measures of each of the angles of the hexagon angles to find the sum.
Formative Assessment
Self Check: Analyzing a Hexagon
Complete this Self Check by yourself.
The large figure is a hexagon. Figures ABGF andCDEF are parallelograms.
- Find the measures of ∠1, ∠2, ∠3, ∠4, and ∠5.
- Explain how you determined each angle measure.
- What is the sum of the angles in the hexagon? How do you know?

Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to get an idea of the connections that students see between triangles, quadrilaterals, and other polygons.
ELL: The “Reflect On Your Work” section provides opportunities for ELLs to develop literacy in English and proficiency in mathematics. Make sure students use both academic and specialized mathematical language when reflecting on their learning at the end of each session. Give students time to discuss the summary before they write.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
When I look at triangles, quadrilaterals, and other polygons, I see these connections …