Graphing A Table Of Values

Overview
Students explore the idea that not all straight lines are proportional by comparing a graph representing a stack of books with a graph representing a stack of cups. They recognize that all proportional relationships are represented as a straight line that passes through the origin.
Key Concepts
Not all graphs of straight lines represent proportional relationships.
There are three ways to tell whether a relationship between two varying quantities is proportional:
- The graph of the relationship between the quantities is a straight line that passes through the point (0, 0).
- You can express one quantity in terms of the other using a formula of the form y = kx.
- The ratios between the varying quantities are constant.
Goals and Learning Objectives
- Understand when a graph of a straight line is and when it is not a proportional relationship.
- Recognize that a proportional relationship is shown on a graph as a straight line that passes through the origin (0, 0).
- Make a table of values to represent two quantities that vary.
- Graph a table of values representing two quantities that vary.
- Describe what each variable and number in a formula represents.
Stacks of Cups and Books
Lesson Guide
- Have students examine the diagrams.
- Point out that each diagram shows a stack of a number of objects. Ask students to imagine what would happen to each stack if more objects were added to the stack or if objects were taken from the stack.
Have partners discuss the questions.
Ask pairs to make a prediction about whether the height of a stack of cups is proportional to the number of cups in the stack and whether the height of a stack of books is proportional to the number of books in a stack.
Teacher Demonstration
Demonstrate one or both of the stacks, either with a stack of books of equal width or with cups that have a visible lip. (Paper cups with very thin edging will illustrate the stacking effect well enough if you pose questions that bring out the fact that the height of the stack is determined in different ways by the base of the cup and by the thickness of the edging.)
Mathematics
The key idea is to compare two stacks of objects, one with a height that is proportional to the number of objects (books) in the stack, and one with a height that is not proportional to the number of objects (cups) in the stack. While the height of the stack of cups is represented by a straight line graph (a linear graph), the graph does not pass through the origin, and the ratio between values for the two related quantities—height of the stack and number of cups in the stack—is not constant. Ask students:
- Each situation has multiple quantities. What are the two variable quantities in each situation?
- How can you describe (in words) what happens to one of the quantities when the other quantity increases or decreases?
- What are some pairs of values for the two quantities in each situation?
- Is there a constant ratio between pairs of values in each situation?
ELL: When discussing this example, make a point of writing the questions on the board, along with students’ responses. This will assist ELLs by giving them written and oral access to the questions. Have students write all important information in their Notebook.
Answers
- The height of the stack of cups is not proportional to the number of cups in the stack.
- The height of the stack of books is proportional to the number of books in the stack.
Opening
Stacks of Cups and Books
Discuss the following with your classmates.
- Do you think the height of a stack of cups is proportional to the number of cups in the stack?
- Do you think the height of a stack of books is proportional to the number of books in the stack?
- Make a prediction for each question.

Math Mission
Lesson Guide
Discuss the Math Mission. Students will graph two relationships and determine whether either one is a proportional relationship.
Opening
Graph two relationships and determine whether either one is a proportional relationship.
Stack of Cups
Lesson Guide
Have students work in pairs on all problems and the presentation.
SWD: Go over the mathematical language used throughout the lesson. Make sure students use that language when discussing the problems during Work Time.
Preparing for Ways of Thinking
Listen and look for students who:
- Have different choices about which quantity to put first in the tables (and which to put on each axis for the graphs)
- Move between representations (i.e., table, graph, formula) to make sense of each one in relation to the others
- Discuss and debate about whether the graphs should include more than the coordinate pairs included in the tables
- Discuss whether the relationships are proportional—and what is the constant of proportionality
SWD: When working on abstract concepts of this type, provide as many manipulatives and visual supports as possible to represent students' ideas about the constant of proportionality.
Mathematics
The problems about the stacks of cups and books connect the dots between multiple representations: diagrams, tables, graphs, and formulas. Then students are asked to interpret these representations in relation to the working definition of a proportional relationship, which is developed across the first part of this unit.
Mathematical Practices
Mathematical Practice 2: Reason abstractly and quantitatively.
Look for students who easily move between the meaning of the situation being modeled and the mathematical representations used to model it.
Interventions
Student doesn’t recognize that h and n represent variable quantities.
- As the number of cups in the stack increases or decreases, so does the height of the stack.
- The height of the stack depends on the number of cups in the stack; they vary in relation to one another.
Student doesn’t attend adequately to the difference between the total cup height and the 0.5 centimeter lip of the cup.
- Stack a few actual cups. What do you need to know in order to determine how much the height increases when you add a cup?
Student struggles to create the graphs.
- Recall our work with graphing yesterday.
- Review the demonstration at the beginning of the previous lesson.
Student doesn’t relate the given formulas to the tables or the graphs.
- Substitute some of the pairs of values from your table into the formula. Does it work if you substitute n-values for x and h-values for y or the other way around? What does this tell you?
- Look at the points on your graph. Does the formula give you the coordinates for each point?
Student doesn’t know how to identify the constant of proportionality or understand its meaning.
- Look at the pairs of values in your tables.
- Refer to your summary notes from previous lessons.
Answers
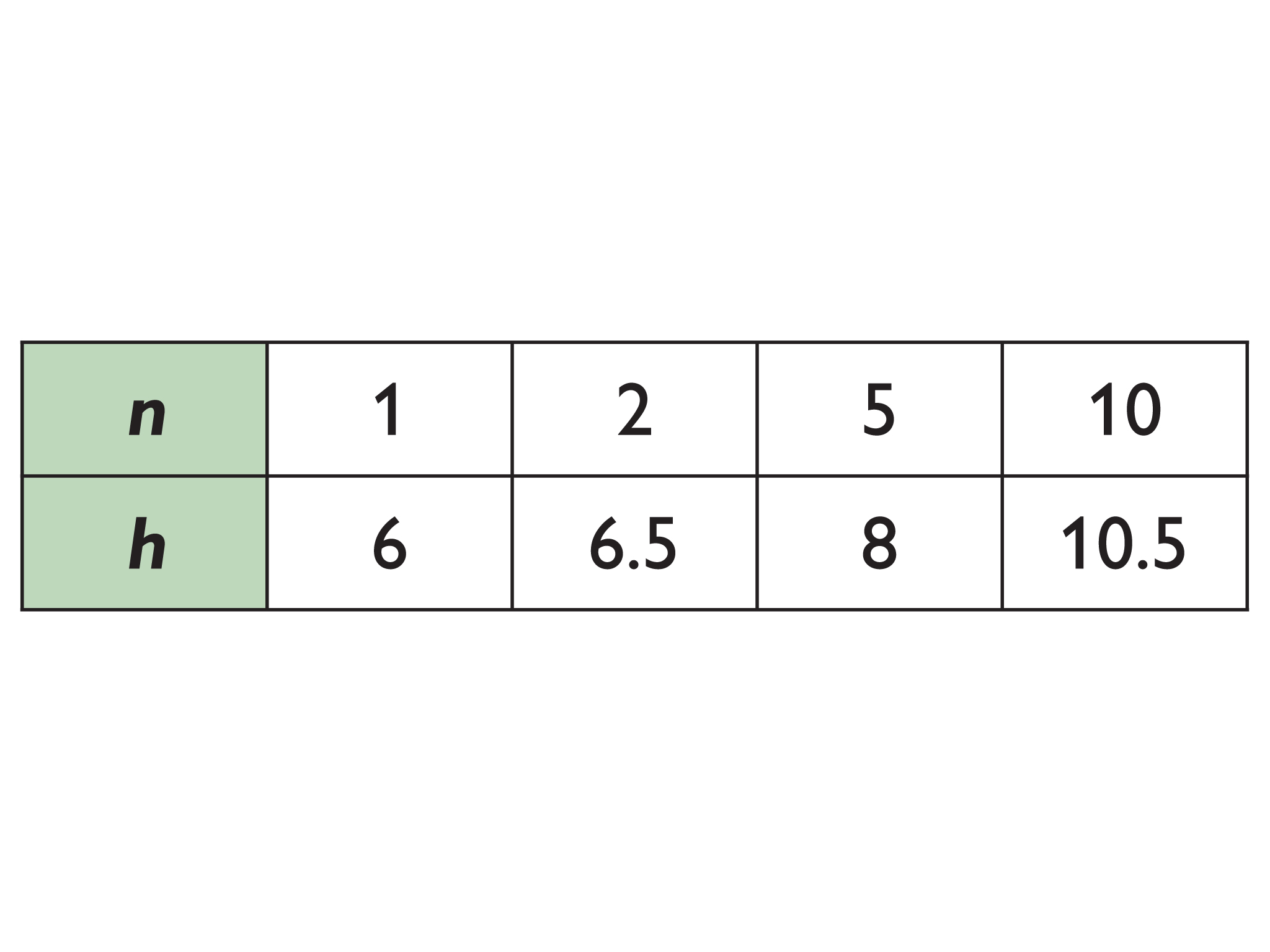
- Note: Tables can be vertical or horizontal, with either quantity, n or h, first.
- Note: It is fine if students who put h first in their table put h on the horizontal axis and n on the vertical axis, as long as the points of their graphs correspond to this positioning.
- In the formula h = 0.5n + 5.5, h is the height of the stack, n is the number of cups in the stack, 0.5 is the thickness in centimeters of the part of each cup that sticks up when they are stacked, and 5.5 is the height in centimeters of the base of the cup without the lip that sticks up.
Work Time
Stack of Cups
- Make a table that relates h (the height of a stack of cups) to n (the number of cups in a stack) for stacks of 1, 2, 5, and 10 cups.
- Use your table to make a graph that shows the relationship between the height of the stack of cups and the number of cups.
- If you have at least one cup, the formula for the relationship between the height of the stack, h, and the number of cups, n, is:
h = 0.5n + 5.5 - Describe what each variable and each number in the formula represents.

Hint:
Look at the image of the stack of cups.
- What does 0.5 represent?
Think about the problem situation.
- What does 5.5 represent?
- What does h represent?
- What does n represent?
Stack of Books
Lesson Guide
Have students work in pairs on all problems and the presentation.
Interventions
Student doesn’t recognize that h and n represent variable quantities.
- As the number of books in the stack increases or decreases, so does the height of the stack.
- The height of the stack depends on the number of books in the stack; they vary in relation to one another.
Student struggles to create the graphs.
- Recall our work with a graphing application in the previous lesson.
- Review the demonstration at the beginning of the previous lesson.
Student doesn’t relate the given formulas to the tables or the graphs.
- Substitute some of the pairs of values from your table into the formula. Does it work if you substitute n-values for x and h-values for y or the other way around? What does this tell you?
- Look at the points on your graph. Does the formula give you the coordinates for each point?
Student doesn’t know how to identify the constant of proportionality or understand its meaning.
- Look at the pairs of values in your tables.
- Refer to your summary notes from previous lessons.
Answers


Note: Tables can be vertical or horizontal, with either quantity n (number of books) or h (height in inches), first.
Note: It is fine if students who put h first in their table put h on the horizontal axis and n on the vertical axis, as long as the points of their graphs correspond to this positioning.
- In the formula h = 0.5n, h is the height of the stack, n is the number of books in the stack, and 0.5 is the thickness in inches of a single book.
Work Time
Stack of Books
- Make a table that relates h (the height of a stack of books) to n (the number of books in a stack) for stacks of 1, 2, 5, and 10 books.
- Use your table to make a graph that shows the relationship between the height of the stack of books and the number of books.
- The formula for the relationship between the height of the stack, h, and the number of books, n, is:
h = 0.5n - Describe what each variable and the number in the formula represents.

Hint:
Look at the image of the stack of books.
- What does 0.5 represent?
Think about the problem situation.
- What does h represent?
- What does n represent?
Prepare a Presentation
Preparing for Ways of Thinking
Listen and look for students who:
- Have different choices about which quantity to put first in the tables (and which to put on each axis for the graphs)
- Move between representations (i.e., table, graph, formula) to make sense of each one in relation to the others
- Discuss and debate about whether the graphs should include more than the coordinate pairs included in the tables
- Discuss whether the relationships are proportional—and what is the constant of proportionality
Answers
- The graph of the proportional relationship intersects the vertical axis at (0, 0) the origin.
Challenge Problem
Answers
- It wouldn’t make sense to have a part of a cup or part of a book in a stack, so the n-values in each case are only whole numbers. The graph has points with only positive whole-number n values.
Work Time
Prepare a Presentation
You know that the graph of a proportional relationship is a straight line. What do you notice about where the graph of a proportional relationship intersects the vertical axis?
- Compare your graph of the stack of cups to your graph of the stack of books. Prepare a presentation about your findings. Justify your thinking.
Challenge Problem
- Look at the graph you made for the stack of cups and the stack of books. Each one of your graphs should consist of separate points that are not connected by a line. Explain why.
Hint:
In particular, what is different about your two graphs? What does this difference tell you?
Make Connections
Lesson Guide
Showcase tables and graphs from students who ordered the quantities differently to explore the consequences (and validity) of each ordering. Then highlight the work of students who made productive use of the meaning of the situation and made use of multiple representations in order to make sense of their work. Finally have students compare interpretations of the formulas for each situation and interpretations of the graphs.
- (Compare the graphs from the students who put the height on the horizontal axis.) Is the graph still a straight line? Is the proportional relationship proportional either way?
- How did the situation help you interpret the formulas?
- How did the situation help you interpret the graphs?
SWD: As students are comparing the two graphs, write down any key terms and information that arise in their discussion. Keeping a list of key terms and information is a good way to go back and clarify any misconceptions students may have.
ELL: Be sure that your pace is appropriate when posing these questions, especially when interacting with ELLs.
Performance Task
Ways of Thinking: Make Connections
Take notes about your classmates’ presentations of their graphs.
Hint:
As your classmates present, ask questions such as:
- What does each variable and number in the formula for the stack of cups represent?
- What does each variable and number in the formula for the stack of books represent?
- How are the two formulas similar? How are they different?
- Can you explain how you made your table?
- How did you use your table to make your graph?
- How do your predictions from the beginning of the lesson compare to your findings?
- What do you know about the table of values that define a proportional relationship?
- What do you know about the graph of a proportional relationship?
- When does the graph of a straight line not define a proportional relationship?
Identify Proportional Relationships
Lesson Guide
- Have pairs quietly read and then discuss how to identify proportional relationships.
- As student pairs work together, make a note to clarify any misunderstandings in the class discussion.
- After a few minutes, discuss the summary as a class. Be sure students understand that even if the graph of the relationship between two varying quantities is a line, the relationship is only proportional if the line passes through the point (0, 0), the origin.
SWD: Thinking aloud is one strategy for making learning visible. When teachers think aloud, they are externalizing their internal thought processes. Doing so may provide students with insights into mathematical thinking and ways of tackling problems. It also helps to model accurate mathematical language.
Formative Assessment
Summary of the Math: Identify Proportional Relationships
Read and Discuss
- Being able to identify proportional relationships is important in mathematics.
- There are three ways that you can tell whether the relationship between two varying quantities is proportional:
- If the graph of the relationship between the quantities is a line that passes through the point (0, 0), then the relationship between the quantities is proportional.
- If you can express one quantity in terms of the other by using a formula of the form y = kx, then the relationship between the quantities is proportional.
- If the ratios between the varying quantities is constant, then the relationship between the quantities is proportional.
- Remember that even if the graph of the relationship between two varying quantities is a line, the relationship is only proportional if the line passes through the point (0, 0).
Note: Sometimes proportional relationships are said to be directly proportional.
Hint:
Can you:
- Describe three ways that you can tell whether a relationship between two varying quantities is proportional?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of the class. Review the reflections to find out how students know that the graph of a proportional relationship is different from the graph of a non-proportional relationship.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
One way that the graph of a proportional relationship is different from the graph of a non-proportional relationship is …
