Multiplication Properties of Equality

Overview
Review the multiplication property of equality. Demonstrate the use of “ask myself” questions to understand a problem before solving it. Have students discuss the strategies that they can use when they feel stuck on a problem. Direct partners to solve a problem using a ratio table and equations, and then justify their solution in a presentation using the multiplication property of equality. Have each student write a Summary of the Mathematics in the lesson and work together to create a classroom summary.
Key Concepts
Students use the multiplication property of equality to justify their solution to a ratio problem.
Goals and Learning Objectives
- Before starting to work on a problem, make sense of the problem by using “ask myself” questions.
- Persevere in solving a problem even when feeling stuck.
- Solve a ratio problem using two different strategies.
- Link arithmetic and algebraic methods to solve a ratio problem.
- Use the multiplication property of equality to solve ratio problems
Multiplication Property of Equality
Lesson Guide
Review the multiplication property of equality, and have a brief discussion about how it is helpful for solving the footwear store example. Students may not recognize the property by name, but it should be familiar from their work in Grade 6 using equations for ratios. Also discuss how the multiplication property of equality is used in ratio tables. In ratio tables, both numbers, or quantities, in the ratio need to be multiplied by the same value c to ensure that the ratios are equivalent.
Opening
Multiplication Property of Equality
The definition of the multiplication property of equality states:
If a = b, then a ⋅ c = b ⋅ c.
Discuss the following with your classmates.
- Where is the multiplication property of equality used in this example?
- How would you use a ratio table to solve this problem?

“Ask Myself” Questions
Lesson Guide
Ask students to silently read the instructions and example problem. Have one student explain in her own words what the problem is asking.
Tell students that today, and most days, they will work on problems on their own and then they will discuss their ideas with a partner.
Show students how to copy the problem to their Notebook. Then demonstrate how to use “ask myself” questions to understand the problem:
- If I looked at the example problem, I would start by asking myself questions that will help me understand the problem. Here are the problem instructions—I’ll start with those. “Solve the problem using a ratio table and using an equation. Describe how you used the multiplication property of equality to solve the equation.”
- We used ratio tables before, but what does it mean to use an equation to solve the problem? That probably just means to write an equation. I’ll have to look at the example problem closer to understand what that really means.
- What does it mean to use the multiplication property of equality? Well, we talked about that a little bit in the Opening. I am using this property whenever I am multiplying both of the ratio quantities.
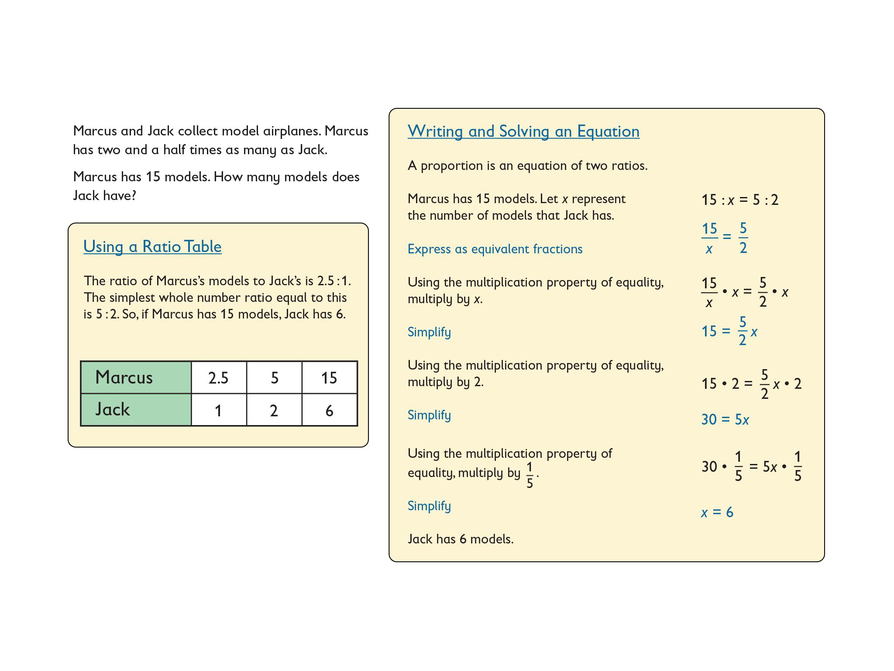
- What is the problem asking me to do? Let me read the example problem and then restate the problem in my own words—I know that is often helpful. Hmmm…it seems to be about model airplanes.
- What kinds of comparisons is the problem looking at? It seems to compare how many models Marcus and Jack have.
- What are the numbers in the problem and what do they mean? I see “two and a half times” in the problem. It is saying that Marcus has two and a half as many models as Jack does. But there is also this number: Marcus has 15 models.
- What is the problem asking for? Oh, I see: “How many models does Jack have?” I need to figure that out during these different solution methods.
After the demonstration, ask students:
- What questions can you ask yourself to make sense of a problem?
- What can you do if you get stuck on a problem?
First, have students spend a few minutes thinking about these two questions on their own. Then have students discuss their ideas with their partner.
When students are done, have them share their ideas with the class. As with previous lessons, having students generate their own ideas allows them to take ownership of their own learning. If students are having trouble thinking of questions, give them a list of “ask myself” questions to refer to.
These Hints are ideas for students to use for “ask myself” questions:
- What does ___ mean?
- What is this problem talking about?
- What kinds of comparisons is the problem looking at?
- What are the numbers in the problem, and what do they mean?
- What is the problem asking for?
These Hints are ideas for things students can do if they get stuck on a problem:
- Look at similar problems you have solved previously.
- Model the problem using counters or other materials.
- Sketch a diagram or other representation.
- Write what you do know.
- Write questions to ask later.
- Check other resources.
Record students’ ideas and project them for the class as two separate lists. After all ideas are listed, review each one for clarity. Agreement is not necessary because having a diversity of ideas is useful. These lists of ideas can continue to grow throughout the year.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Explain that it is important for students to first make sense of a problem before beginning to solve it and to persevere in solving the problem even if they feel stuck.
Opening
“Ask Myself” Questions
When working by yourself, you should:
- Make sense of the problem.
- Use “ask myself” questions to see what you need to understand before starting.
- Persevere through difficulty by using what you do know.
Read the worked problem. Then watch your teacher give an example of how to use “ask myself” questions to understand the problem.
- Solve the problem using a ratio table and using an equation.
- Describe how you used the multiplication property of equality to solve the equation.
Hint:
Here are ideas for “ask myself” questions:
- What does ____ mean?
- What is this problem talking about?
- What kinds of comparisons is the problem looking at?
- What are the numbers in the problem and what do they mean?
- What is the problem asking for?
Here are ideas for what to do if you get stuck:
- Look at similar problems you have solved previously.
- Model the problem using counters or other materials.
- Sketch a diagram or other representation.
- Write what you do know.
- Write down questions to ask later.
- Check other resources.
Math Mission
Lesson Guide
Discuss the Math Mission. Students will compare different strategies for solving a ratio problem.
Opening
Compare different strategies for solving a ratio problem.
Use Different Strategies
Lesson Guide
Have students work on both Work Time problems on their own for 5 minutes before working with their partner.
ELL: Having students work in groups allows teachers to monitor individual student progress by listening to and recording student conversations and peer problem solving. This type of collaborative work gives ELLs the opportunity to use mathematical language and to engage in conversation with their peers.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
Students begin their work by first making sense of the problem by using “ask myself” questions. Then students persevere by using the ideas they generated for what to do when they get stuck.
Interventions
Student does not start with “ask myself” questions.
- What questions did you ask yourself before you started solving this problem?
Student stops working when he or she gets stuck.
- What can you do if you get stuck on a problem?
Student changes the order of subtraction or division.
- Why can you change the order of the numbers for addition and multiplication but not for subtraction and division?
Possible Answers
Answers will vary. Possible ratio table:
 Possible equation solution: Let x be the number of nurses that are needed at the hospital. 1:12 = x:672. If I rewrite as fractions:
Possible equation solution: Let x be the number of nurses that are needed at the hospital. 1:12 = x:672. If I rewrite as fractions: The hospital needs 56 nurses for the 672 patients.
- I used the multiplication property of equality to multiply the equivalent fractions by 672.
Work Time
Use Different Strategies
Work on your own to solve this problem using a ratio table and using an equation. Then work with a partner.
A local hospital has a rule that the ratio of nurses to patients must be 1 : 12. A hospital expands to fit 672 patients. How many nurses does the hospital need?
- Explain your strategies to your partner. Challenge your partner to have clear and complete explanations.
- Describe how you used the multiplication property of equality to solve the equation.
Hint:
- What questions did you ask yourself before you worked on this problem?
- Remember to multiply both ratio quantities by the same value to preserve equality.
- The multiplication property of equality states that if you multiply both sides of an equation by the same quantity, the sides remain equal.
Prepare a Presentation
Lesson Guide
Have partners work on the presentation together. Remind students to think about the qualities of an effective presentation. If they would like to, students can refer to the previously shared hints about how to prepare a clear presentation.
ELL: Allow ELLs to write up parts of their answers. It can be hard for ELLs to explain the whole phrase, but they can either draw what they mean or use their diagram from the interactive. This will help them prepare for the Ways of Thinking sections of the lesson. Allow students to annotate notes next to their drawings.
Preparing for Ways of Thinking
Students use two strategies to solve a ratio problem and explain how the multiplication property of equality is relevant. Look for students who used different ratio tables to solve the problem. Ask other students who wrote different equations also to share their presentations. It is helpful to also include incorrect strategies in the set of presentations students consider. Have these students discuss their approaches during Ways of Thinking.
Challenge Problem
Answers
- Answers will vary. Possible answers:

Let g represent greeters.
Let s represent servers.
- For both the greeters and servers calculations, the multiplication property of equality is used to multiply both sides of the equations by the denominators of both ratios. For the greeters, the denominators in the equation are 5 and g; for the servers, the denominators in the equation are 11 and s.
Work Time
Prepare a Presentation
- Compare how your strategies for solving the problem are similar and different.
- Justify your solution using the multiplication property of equality.
- Identify any mistakes you made and what you learned from them.
- Include any questions your partner asked about your explanation.
Challenge Problem
Tips at a restaurant are split among employees. The ratio of tips earned by servers to greeters to clean-up team is 11 : 5 : 2. The clean-up team earned $20.80 from tips one night.
How much did the servers and greeters earn from tips in the same night?
- Solve the problem using a ratio table.
- Solve the problem using an equation.
- Identify where you use the multiplication properties of equality in your solutions.

Make Connections
Lesson Guide
This lesson is designed to make connections between arithmetic and algebraic methods of solving ratio problems. It is not critical that all students are able to solve the problem algebraically at this stage. They should, however, have a good grasp of the arithmetic methods used.
For each problem, choose two student presenters who reached the same conclusion about the result of the problem but who did not have the same ratio table and equation steps. Ask the class to compare the steps of the two solutions. Spend time discussing errors so that everyone has the opportunity to learn from the mistakes.
Spend a few moments discussing how the multiplication property of equality is useful in students’ justifications.
If you have time, ask two students who completed the Work Time Challenge Problem to present their work exploring this complex ratio problem.
Mathematical Practices
Mathematical Practice 1: Make sense of problems and persevere in solving them.
- Encourage students to talk about the way they made sense of the problems and any strategies they used to persevere when stuck on a problem.
Performance Task
Ways of Thinking: Make Connections
Take notes about how your own strategies to solve the ratio problem are similar to and different from your classmates’ strategies.
Hint:
As your classmates present, ask questions such as:
- Did you find it more difficult to use the ratio table or the equation to solve the problem?
- How is your way of solving the problem with an equation similar to using a ratio table?
- Why does the multiplication property of equality help you solve the equation?
What Is a Good Summary?
Lesson Guide
Begin this activity with a brief discussion about the qualities of a good summary:
- It focuses on the important mathematics in today’s lesson.
- It uses a few sentences to explain the mathematics.
- It goes beyond the answers to the bigger ideas in the lesson.
Have each student write a Summary of the Math in the lesson, and then work together to write a class summary. When done, if the class summary is helpful, record and share the summary with the class.
A Possible Summary
Multiply both quantities in the ratio by constant c to find an equivalent ratio. This is true whether you are using a ratio table or equation. Both methods also show the steps used to solve the problem. In the ratio table, the columns show the order of the steps. In the equation solution, the steps are shown in the set of equations written to solve the problem. The difference is that the equation uses a variable to represent the unknown value. The multiplication property of equality is useful when working with ratios because the use of multiplication is needed to write equivalent ratios. Justify means to explain the reasons in a logical way.
Additional Discussion Points
Additional ideas you might want to discuss are:
- It is necessary to use units to explain the meaning of quantities in real-world situations. Ratios do not have units when referring to mathematical relationships in general. The numbers 1 and 2 have the same ratio relationship as 4 and 8.
- Other properties of equality may be used in algebraic thinking, for example, addition or subtraction properties of equality.
SWD: Refer to the Hint questions as a checklist of the information students need to include in their summaries. Create a digital or paper resource of the questions for students to keep in front of them as they write their summaries. For some students, navigating back and forth between the questions, Hints, and their written work will be confusing and distracting.
Formative Assessment
Summary of the Math: What Is a Good Summary?
A good summary clearly explains important mathematics of today's lesson.
- Write a summary comparing different strategies for solving the ratio problem.
Hint:
Check your summary.
- Do you describe how the different strategies for solving the ratio problem are similar and different?
- Do you explain why the multiplication property of equality is useful for solving ratio problems?
- Do you define justify?
Reflect On Your Work
Lesson Guide
Have each student write a brief reflection before the end of class. Review the reflections to learn if students understand why the multiplication property of equality is useful. Record any wonderings and other reflection comments to share with the class as appropriate.
Work Time
Reflection
Write a reflection about the ideas discussed in class today. Use the sentence starter below if you find it to be helpful.
The multiplication property of equality is useful because…