- Author:
- Marguerite Dasso
- Subject:
- Educational Technology, Algebra
- Material Type:
- Lesson Plan
- Level:
- Middle School
- Grade:
- 8
- Tags:
- License:
- Creative Commons Attribution Non-Commercial
- Language:
- English
- Media Formats:
- Interactive, Video
Education Standards
Understanding Slope Intercept Form
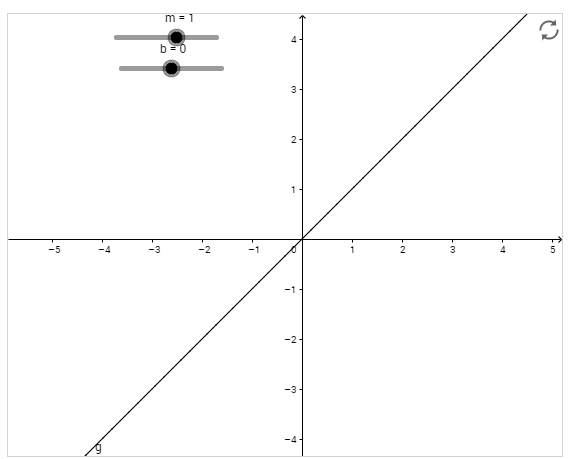
Overview
OLO: Students will be able to explain how changing the y-intercept and slope will change the appearance of the line.
This lesson is to help students develop the relationship between slope(m) and y-intercept(b) by using an interactive coordinate plane to explore. This is a 2 part lesson with some teacher clarification in between the 2 parts. The teacher component in between the 2 parts is to make sure the students fully understand the relationships developed in part 1 before applying it to part 2.
If you have a Face to Face class and just want a print out/editable version for Google Classroom Click Here
What is m? What is b?
For the 1st part of this activity the students are in full exploration mode. You may or may not tell the student what m and b stand for before this lesson. The hope is that they get a conceptual understanding of how the values change the graph, and don't necessarily need to know that m represents slope, and b represents y-intecerpt.
1) Go to the following site :
http://www.oercommons.org/courses/slope-intercept-form/view
2) Start with moving the m first.
What happens to the line when m is positive?
What happens to the line when m is negative?
What happens to the line when m is close to zero?
What happens to the line when m is close to 5?
What happens to the line when m is close to -5?
What is happening to the line when you change m?
3) Now move just the b.
What happens to the line when b increases?
What happens to the line when b decreases?
What is happening to the line when you change b?
4) What does m stand for?
5) What does b stand for?
Identifying parts of the Equation
If you have the chance at being Face 2 Face pull the class back together to discuss the y = mx + b equation and discuss each of the parts of the equation. This will serve as a way to make sure that every student developed the correct assumptions from part 1. Sometimes students miss the mark and need to be steered in the correct directions before they can continue onto part 2. If you do not have a chance to be face to face for discussion try this video instead.
Check out this video for an explanation of Basic Linear Functions.
Assessment: Can Identify the parts of the equation and how it relates to the graph?
Students will be using the website from Task 1 to test out their newly/confirmed skills from part 1 and 2. If students do not notice the connection between m and b, add additional questions to help them get to the end.
Add these questions for students that don't get the final 2 questions correct?:
- What equations have an uphill slope?
- What equations have a downhill slope?
- What equations are flat?
- What connection can be made between the slope and the type of line?
- Would you rather walk up a hill with a slope of 1 or 10? Why?
- What equations are above the origin?
- What equations are below the origin?
- What equations are on the origin?
- What connection is there between the equation and where the line falls in relation to the origin?
y = mx + b
For each equation below, go back to http://www.oercommons.org/courses/slope-intercept-form/view if this website does not load use www.desmos.com
Identify each m and b from the equation below and slide the m and b cursors to match. Then bold all of the descriptions that apply below, feel free to cross out/delete the ones that don't apply. See the first example is done for you.
y = 2x - 1 m = __2___ b = ___-1___
Uphill downhill flat above the origin on the origin below the origin proportional
y = 3x m = ________ b = _______
Uphill downhill flat above the origin on the origin below the origin proportional
y = 2.5x + 3 m = ________ b = _______
Uphill downhill flat above the origin on the origin below the origin proportional
y = x m = ________ b = _______
Uphill downhill flat above the origin on the origin below the origin proportional
y = 2 m = ________ b = _______
Uphill downhill flat above the origin on the origin below the origin proportional
y = -3x + 4 m = ________ b = _______
Uphill downhill flat above the origin on the origin below the origin proportional
y = 2.3x - 2 m = ________ b = _______
Uphill downhill flat above the origin on the origin below the origin proportional
y = -5 m = ________ b = _______
Uphill downhill flat above the origin on the origin below the origin proportional
y = -4x + 4 m = ________ b = _______
Uphill downhill flat above the origin on the origin below the origin proportional
y = -2x m = ________ b = _______
Uphill downhill flat above the origin on the origin below the origin proportional
- How do you know without graphing if the line will go downhill? uphill? Flat?
- How do you know without graphing it if the line is above the origin? On the origin? Below origin?